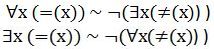Закон тождества, как и любой закон логики, тавтологичен: X=X  (что верно при каждом значении Х)
Отрицание тавтологии - противоречие: not X=X (что ложно при каждом значении Х)

Когда в формальной логике пишут (для значений True, False переменной X): X and not X = False
то это ничто иное, как: False and not False = False

Последняя запись может быть выражена иначе: not (False=False) and (False=False) = False
Или, еще короче, как: not (False=False)=False  т.е. (False≠False)=False

Предикат равенства Х=Y возвращает либо истину, либо ложь (в зависимости от того, что в эти переменные подставляется).  Иначе говоря, эти 2 варианта можно выразить так: Х равно Х, что всегда истинно; Х не равно Х, что всегда ложно.

Ссылка лекцию: https://www.youtube.com/watch?v=FXtxcGne8S0

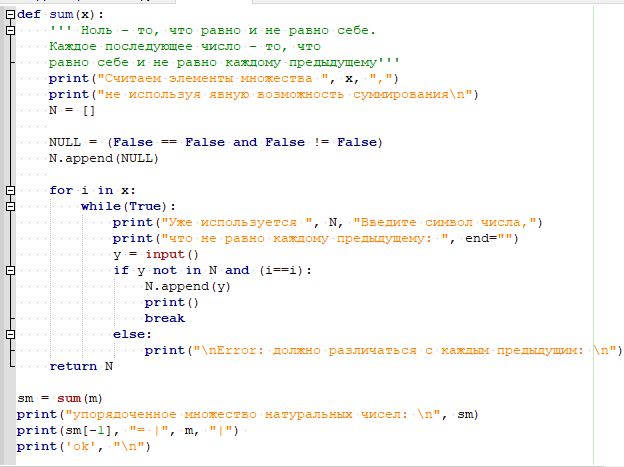
Ничто = (ничто = не ничто), т.е NULL = (NULL = not NULL)

Пока есть ничто, и должно возникнуть нечто. 

Как? Через отрицание ничто ...

Нечто = не ничто, т.е. 1 = not null

Жизнь - механизм (в кибернетическом смысле) поиска того, что повторяемо.
Извлекая законы (т.е. извлекая то, что повторяемо) и имея возможность выбирать
между различными целями (состояниями в будущем) -
позволяет этому механизму самовоспроизводиться с усложнением. 

Как это формулируется математически? Очень просто. 
Функция в математике этот смысл как раз отображает y = f(x):
если к аргументу функции применить функцию, то получим ТОЛЬКО значение функции.

Могут ли числа "a" и "b" для 9a + 7B = 111 быть четными?
Поскольку 111 нечетно, то (9a + 7B) тоже нечетно.
Эта сумма может быть нечетна только если одно слагаемое нечетно, а другое четно.
Вариант, когда оба нечетны, отпадает по той простой причине, что:
(2k +1) + (2m + 1) = 2(k + m + 1) тоже четно.
Допустим, 9а нечетно. Тогда 9а = 8а + а. Следовательно "а" нечетно.

#include <iostream>
using namespace std;

def sum(x):

    ''' Ноль - то, что равно и не равно себе.
    Каждое последующее число - то, что
    равно себе и различается с каждым предыдущим'''
    print("Считаем элементы множества ", x, ",")
    print("используя возможность суммировать единицы")
    y = (False != False)
    for i in x:
        y = (i == i) + y
    return y

Число ноль - число. Число один - число. 
При этом неверно, что:
(число ноль = число), (число один = число).

Здесь имеет место быть предикация P(x): 
число(число ноль), число(число один).

Так что же такое число, число как таковое? Там, где в вещах и явлениях отмечаются отношения "быть равным", "быть различным", там имеем дело с числом. 

Зависят ли эти отношения (равняться, различаться) от нашего понимания или непонимания? Нет. 

Тезисно из передачи с участием Семихатова о теории струн. Заголовок - оттуда же.

1. принцип неопределенности - чем определенней координата частицы, тем менее определенней ее направление (и наоборот)

2. квантовой гравитации не существует, квантовоя гравитация существовала в начале вселенной
 

СУЩЕСТВУЕТ ли колесико (рис. ниже), которое бы крутилось? Допустим, одно из них крутиться. Тогда рядом находящееся колесико должно крутиться в другую сторону.

Поскольку колесиков четное количество, то это же колесико, которое крутится в одну сторону, должно крутиться и в другую сторону.