Предикация существования и законы де Моргана

Субъект - предикат (о чем говорится - что говорится)
Примеры 1.1 и 1.2 - примеры того, что существует.
1.1 четырехугольник с прямыми углами - четырехугольник
1.2 четырехугольник с прямыми углами - с прямыми углами
Предикация существования
2.1 (Х равно Х) - равно,
т.е. (Х существует) - существует
2.2 (Х не-равно Х) - не-равно,
т.е. (Х не существует) - не существует
#Примеры:
find_in_set('d', {'a', 'b', 'c'})
#нет 'd' в множестве {'a', 'b', 'c'}
#нет 'd' в множестве т.к. (каждое Х не-равно d)
find_in_set('d', {'a', 'b', 'c', 'd'})
#есть 'd' в множестве {'a', 'b', 'c', 'd'}
#есть 'd' в множестве т.к. (хотя бы одно Х равно d)
Законы де Моргана применительно к предикату 'существует'
принимают вид:
(Верно, что каждое Х - существует) эквивалентно тому, что (неверно, что хотя бы одно Х – не существует)
(Верно, что хотя бы одно Х - существует) эквивалентно тому, что (неверно, что каждое Х – не существует)
- bulygin69
- Для комментирования войдите или зарегистрируйтесь

Комментарии
def find_in_set(V, lst):
#V - что ищем в множестве lst
#lst - множество, в котором ищем V
#т.е. считаем сколько V в lst
exist = False
for X in lst:
#для каждого элемента X множества lst
#проверяем х=v
if X == V:
exist = True
if exist:
print('есть', V, 'в множестве lst т.к. (хотя бы одно Х равно V)')
else:
print('нет', V, 'в множестве lst т.к. (каждое X не-равно V)')
#Примеры:
find_in_set('d', {'a', 'b', 'c'})
#нет 'd' в множестве {'a', 'b', 'c'}
#нет 'd' в множестве т.к. (каждое Х не-равно d)
find_in_set('d', {'a', 'b', 'c', 'd'})
#есть 'd' в множестве {'a', 'b', 'c', 'd'}
#есть 'd' в множестве т.к. (хотя бы одно Х равно d)
P.S. Верность можно проверить на http://rextester.com/l/python3
Формальная запись законов де Моргана применительно к предикату (существует, не существует)
Как записать, что X относится к Y? В математике пишут xRy. И имеют ввиду, что объект Х относится к объекту Y. Причем считается, что множество объектов и множество отношений не сводится друг к другу.
Но попробуем взгляуть на это иначе. Что, если как Х, так и Y, тоже являются отношениями? Пусть, например, X=(zRk) и Y=(wRp). Возникает вопрос: что будет является тем первичным, из которого можно строить все эти x,y,z,k,w,p и т.д?
Другими словами, подавляющее больштнство из нас, включая математиков, привыкли думать, что мир состоит из атомов (в философском смысле). Другие считают, что первично отношение. Мое мнение: первично отношение. И это отношение - это отношение (быть, не быть).
В частности, чтобы вывести ряд натуральных чисел, достаточно оперировать понятиями (быть, не), т.е. понятиями (существует, не).
Визуально, иерархия понятий: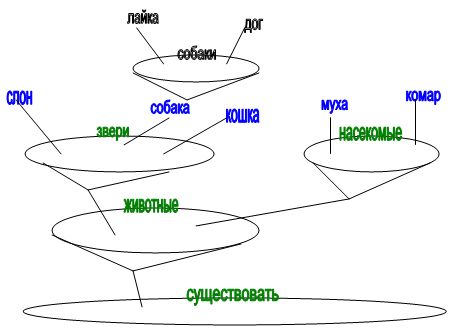
P.S. Диаграммы Венна являются частным случаем такого представления (если смотреть сверху вниз)
Не могу утверждать с полной уверенностью, но Ваше утверждение полность совпадает с тем, что я здесь пропагандирую. Если Вы знакомы с эйдосами от Виктора Сахно (Victor), то это будет означать следующее. Вот пример эйдоса:
В строке "полагание - единица - ряд - группировки (разряда) - представление" в моём представлении самым важным является символ " - ", то есть вот как раз там то всё самое интересное и происходит (в частности там не работают ни законы ФЛ, ни законы сохранения). Как говорит Дмитрий (axby1), осталось правильно открыть кавычки. Вот здесь кусочек дискуссии (цитата оттуда же): ссылка .
Да, я читал. Согласен и с вами, и с Виктором (с Лосевым).
vlopuhin, 9 Август, 2017 - 05:48, ссылка
Да, логика просматривается. В верном направлении мыслите.
Считается, что ложь (в логике) - это что-то такое, что требуется всячески избегать.
По крайней мере, так нас учат со школьной парты. И с этим трудно спорить, казалось бы!
Ведь истинно, что 0=0 или, например, что E=m*(с^2).
Но попробуем убрать ложь (а еще точнее: ложную всегда формулу, т.е. противоречие) из дискретной математики. Что получим?
Только труху от всего того многообразия, которым она оперирует. Только то, что True=True. Получим абсолют бесполезноности.
Вывод.
Верно ли, что полнота сущего без (ложной всегда формулы) наряду с (истинной всегда формулой) невыразима? Верно.
Что это даёт? И главное как это применить на практике? Правильно ли я Вас понимаю, что требуется новая логика, то есть нужно что то изменить в мышлении?
Поскольку имеется запрет на противоречие, а выражать то, "что нет" мы как-то должны ... люди просто используют противоречия, явно не называя его:)
def how_many(lst):
#возвращает сколько элементов в списке
#lst - список чего-либо
count = 0
for X in lst:
if X: #т.е. если Х истинно
count += 1
print('count = %d' %count)
return count
#1 пример: сколько элементов в ['a', 'b', 'c']?
#ответ: 3
how_many(['a', 'b', 'c'])
#2 пример: сколько элементов в ['a', '', 'c']?
#ответ: 2
how_many(['a', '', 'c'])
#3 пример: сколько элементов в [0, '', []]?
#ответ: 0
how_many([0, '', []])
P.S. Верность можно проверить на http://rextester.com/l/python3
Попробую перевести это на мой "китайский". На помощь призову векторную алгебру, точнее достаточно будет одного векторного произведения, в котором используется правило буравчика, а он, как известно, бывает либо левый, либо правый (третьего не дано). Так вот если применить обратную логику (заметьте, не отрицание, и даже не отрицание отрицания!), то получится такая картина: ссылка . Это означает, что Реальность может быть только одна единственная (насколько я понял, у Вас это пустое множество?). Грубо говоря, допустим Мы с Вами договорились по какому то вопросу, создали некоторое обособленное информационное пространство любой мерности. Поскольку один вектор взаимодействия между нами уже задействован, то "вывалиться" мы можем в одну Единственную Реальность. То есть сколько бы мы не выёживались, "виртуальное" пространство из нашей n-мерной действительности всегда будет одно и то же. В частности этим можно объяснить почему договорные и естественные системы в Элементарной Философии Евгения Волкова взаимноизолированы: ссылка . Можно ещё добавить, именно по этому я каждый раз просыпаюсь в одной и той же моей действительности, другой просто не физически не дано (правда здесь нужно уточнить, если тот самый договор между нами разрушить, разорвать связь, то результат будет непредсказуем, на практике это называется раздвоение личности, и тогда в какой действительности я проснусь будет загадкой).
Мой китайский: если (Х не существует), то это то же, что (разные Х - это одно и то же)
Можно ли это как то интерпретировать с помощью переменных и функций (та самая мощность множества по Кантору)?
Моё предыдущее сообщение прошу читать так:
(Х равно не-Х) - не-равно
(Х не-равно Х) - не-равно
Вот эту False (не-равно) в этих (всегда ложных формулах) и используем.
P.S. К Кантору это не имеет отношения.
Не понятно, как используем False (не-равно) ? Другими словами какой смысл вкладывается, может быть это знакоместо, которое в Булевых формулах не участвует? Или высокий импеданс (пофиг что на входе, на выходе установим то, что нужно)?
Уже писал по этому поводу. Математика (логика) замечательна тем, что ее не интересует, что может быть этим Х.
Смысл же (Х равно Х) в том, что это то же, что (Х есть). А смысл (Х не-равно Х) в том, что (нет такого Х, который бы не равнялся себе)
#!/usr/bin/python
# Листинг №3
# логика: (не существует Х) = (Х ≠ Х)
# (существует Х) = (Х = Х)
A = ('a', 'b', 'c', 'd')
B = ('e', 'c', 'd', 'f')
C = ('g', 'h')
D = ()
#
def set_intersect(set_1, set_2):
si = False
for in1Set in set_1:
for in2Set in set_2:
if in1Set == in2Set:
#in1Set == in2Set - т. е. одно,
# т. е. (существует Х) = (Х = Х) = (одно Х)
#print(set_1, и set_2 пересекаются: ', in1Set, '=', in2Set)
si = True
#else: print('пересечение set_1 и set_2 пусто')
#поскольку (не существовать = нет хотя бы одного)
# (не существовать = не (один или более одного))
if si == True: print(set_1, ' и ', set_2, 'пересекаются')
else: print(set_1, ' и ', set_2, ' не пересекаются')
return si
#
set_intersect(A, B) #True: множества A и В пересекаются по элементам 'c', 'd'
#Имеем (одно или более одного) равенства.
set_intersect(A, C) #False: множества А и С не пересекаются,
#поскольку каждый из элементов множества А
#попарно не равен каждому элементу из множества С.
set_intersect(D, D) #False: пустое множество определяется
#тождественно ложной формулой (противоречием).
#В пустом множестве нет такого элемента X, что X=X.
#Сказать, что в множестве не существует элементов -
#то же, что сказать, что
#каждый элемент Х этого множества такой, что Х≠Х.
P.S. Верность можно проверить на http://rextester.com/l/python3
Сам код копировать отсюда https://github.com/bulygin69/exist/blob/master/l3.py
Число и только число! Так что смысл обязательно должен быть, и он заложен в аксиомы.
Может быть речь идёт о множестве мнимых (комплексных) чисел? То есть можно ли противоречие Х≠Х заменить на i*X? По моему логика от этого не пострадает.
Не обязательно. Математика - это не только числа.
Разумеется. Смысл в том, как логически выразить быть и не-быть. И как логически выразить более сложные конструкции, элементами которых являются эти быть и не-быть. Механизм давно известен: Y=F(X) т.е берется Х, применяется к нему F и получается Y.
Знак равенства между Х≠Х и i*X я бы не ставил.
Вот снова хороший пример отношения. (с ужасом ожидаю дальнейшего расхождения во взглядах) Функциональный оператор F является отношением Х и У, а сама формула - наполнением этого отношения.
Мне не нужны какие-то лишние слова. Определение должно их минимизировать.
Поэтому Y=F(X) - 'это
Y - то же самое, что Х, если к Х применить F
Да, согласен. Но я это написал в контексте нашего обсуждения отношений. Вы ведь затеяли дискуссию о том, что отношения лежат в основе всего.
Y и Х - тоже отношения, а не только F, =
Если вы и на этом заостряли внимание, то я не обратил внимания. Если можно, объясните, в чем суть. Вы хотите сказать, что У это отношение каких-то К и Р? Тогда можно ли написать К = У(Р)? А если У = яблоко, что мы получим?
Не буду, поскольку это не входит в тему эту статьи (Предикация существования и законы де Моргана)
А, прошу прощения. Я и не заметил, как перешел в другую тему.
Смысл заложен в логику. А аксиомы должны в нее вписаться.
Нет, так заменять нельзя. Скорее Х≠Х можно заменить на Х = i*X. Потому что, как вы верно заметили, Х≠Х это противоречие, а i*X это число, то есть это разные категории.
Да конечно же, имелось в виду не мнимое число, а комплексное. То есть Х≠Х является противоречием только в проекциях комплексного числа на реальность. В переводе на русский это значит, что для сравнения Х с Х необходимо создать копию Х (так уж устроен мир), а копия никогда не равна оригиналу. То есть на основании Х≠Х можно смело утверждать, что Мир не существует. Как Вам такая трактовка неполноты Гёделя?
Вот какие выводы вы делаете на неверных представлениях. А этими выводами вы широко пользуетесь в дальнейших рассуждениях.
Если бы это было не так, то программы, использующие эту логику, просто бы не работали, не выдавали бы верные результаты.
Кстати, о том, что [ноль А = (А не-равно А)], говорил еще один из величайших логиков - Фреге: «0 – это число, соответствующее понятию ‘не равное себе’»
Мы сейчас обсуждаем не программы, а применение выражений из программ в философии и применение философии к уточнению смысла выражений из программ. Как видим, это может быть продуктивно, но нам нужно избегать неочевидных ошибок.
Фреге был великим ученым, что позволяло ему делать экстравагантные заявления, не задумываясь о последствиях. а последствия приходится расхлебывать нам с вами.
Математика с логикой - как раз тот инструмент, который дает результат. И именно такой результат мне нужен в философском смысле, а не фантазии будто я пролетал Марс.
Совершенно с вами согласен. Я потому и присоединился к обсуждению, что заметил интересный смысл в ваших наблюдениях.
Намекаете на Добро и Зло? Или эта ассоциация помимо вашей воли возникла?
намекаю на Гёделя
На что конкретно?
на теорему о неполноте
Я ею не занимался. Простите.
Да, наверно вы правы. Любое нечто существует только в отношении с другим нечто. Только влияя на это другое нечто, оно заявляет о себе, о своем существовании. Если нечто ни на что не влияет, то есть не имеет ни с чем никаких отношений, то мы не можем говорить о его существовании. Согласны? Отсюда мы делаем вывод: существование это пребывание в отношениях. Быть это влиять (на что-то), не-быть это не-влиять.
A= A ... А существует.
Но это существующее А имеет границу с не-А. И этой границей для А и не-А является А=не-А. По ту же строну этой границы существует не-А
Пример неудачный. А = А это не пребывание в отношениях. Это нечто другое.
равно - одно из видов отношений в математике
Вот ссылка
Ра́венство (ОТНОШЕНИЕ равенства) в математике — бинарное отношение, наиболее логически сильная разновидность отношений эквивалентности.
Именно поэтому пример и неудачный. Обратите внимание на слово "бинарное" в определении. В вашем же примере, как я понимаю, вы сравниваете А с самим собой. Я понимаю, если бы вы написали Х = У, если Х = А и У = А.
print('A' == 'A') #True
А=А ... вернет True, т.е.
(А равно А) - равно
Здесь программа. А из примера выше вы хотите вылезти из программы. В программе как раз в выражении А = А подразумеваются две разные А.
нет, не разные (иначе вернет False)
Вы пытаетесь меня понять, выходя из математической логики. Этого делать не нужно. Под А я понимаю то же, что и вы - конкретное число, постоянную, в противоположность переменной Х или У. Если А это константа, то программа никогда не выдаст вам False.
Под А можно понимать все что угодно: как переменную, так и константу (строковую или числовую) .
Если А - это, например, константа 67, то
67=67 вернет True
Если А - это переменная, то она тоже вернет True.
А вот этот пример удачный. Его и используем.
67 = 67 - мы сравниваем две разные (но не отличающиеся) константы. Они подходят для бинарного отношения. Но только в том случае, если они действительно разные, ну как 67 яблок и 67 утюгов. В 67 яблоках есть сущность, которую мы, отсекая все остальное, нашли как число 67. В 67 утюгах то же самое. Это и есть два разных 67. Их можно между собой сравнить.
67, выделенное из 67 яблок, с самим собой сравнить мы не можем, как и 67, выделенное из 67 утюгов, сравнить с собой. Сравнение - бинарная операция. Сравнить можно только с другим.
нет, неверно.
67 равно 67 ... вернет True
67 утюгов = 67 яблок ... вернет False
Вы или действительно не понимаете меня или не хотите понять. Объясните, как может быть неверно
67 утюгов = 67 яблок ... вернет False только если мы сравниваем яблоки с утюгами. Но мы их не сравниваем, мы сравниваем только их количества, поэтому программа всегда вернет True.
Вот вам реальная программа (и она проверяет на равенство не только количество):
print('67 яблок' == '67 утюгов') #False
print('67' == '67')# True
print(67 == 67)# True
print('яблок' == 'утюгов') #False
print('яблок' == 'яблок') #True
print('утюгов' == 'утюгов') #True
Мы отвлекаемся. Я же не утверждаю, что мы не можем сравнивать что-то, кроме чисел. Мы начали говорить о бинарной операции сравнения. Вот я и хочу обратить ваше внимание на ту легкость, с которой в некоторых случаях забывают об этом непременном условии сравнения. Если вы понимаете, о чем я говорю, то вы должны сказать: "нет, я не сравнивал А с самим собой, это были две разные А (А яблок и А утюгов)" или "да, я сравнивал А с самим собой" и тогда дать пояснение, зачем вы так производите бинарную операцию сравнения.
Бинарной она называется потому, что результата сравнения чего-угодно с чем угодно только два, т.е. либо Трue, либо False.
True мы получаем только в том случае, когда сравнивается с собой. False же получаем только в том случае, когда проверятся на равенство с не с собой.
Если субъектов два (т.е. они разные), то в них может быть что-то одно и тоже. Так, P(b) и P(d) - различны, но предикат P у них тот же. Но тогда и говорим, что P=P, хотя (b не-равно d)
Вот и причина вашего заблуждения. На самом деле:
Результатом будет, как я и сказал ранее, что-то одно: либо True, либо False
print('67 яблок' == '67 утюгов') #False для ДВУХ аргументов
print('67' == '67')# True для ОДНОГО аргумента
Не бывает два разных 67, есть только два разных по отношению друг к другу ('67 яблок') ('67 утюгов')
Я и хочу вам разъяснить, что бывает. В 67 яблоках мы можем выделить сущность, заключающуюся в числе 67. То же мы можем сделать и с утюгами. Это две разные сущности, проявляющие одинаковые свойства, это свойства числа 67. Эти две разные сущности мы можем сравнить и результатом сравнения будет высказывание, они одинаковы или нет, то есть для чисел - равны или нет.
И я вам в который раз объясняю и привожу примеры программы, где
67(яблоки), 67(утюги) - не равны
67, 67 - равны.
Но это 67 у 67(яблоки) и у 67(утюги) - одно и тоже.
==================
Два разных 67 - не существует.
Существует одно 67, которое есть как 67(яблок), так и у 67(утюгов)
Возвращает истину лишь сравнение 67=67, а не сравнение 67(яблок) = 67(утюгов)
А я вам говорю, что существует. 67 у яблок и 67 у утюгов это разные 67, а не одно, как вы говорите. Это количества яблок и утюгов. Мы их сравниваем - разные количества. И они могут оказаться одинаковыми. Но мы не можем сравнить 67 яблок как их количество с самим собой. Пока не начали сравнения, яблок для нас Х, а утюгов У, даже если мы знаем, что их по 67. Х = 67 и У = 67. Мы сравниваем не 67 с 67, а Х с У. В этом смысл бинарности.
Вы пока не отвечайте мне, давайте перенесем это на завтра. Потому что мне нужно снова приводить те же аргументы, которые я уже использовал. А завтра повторимся, может быть другие слова найдутся.
1) это 67 у них одно
2) яблоки и утюги - разные Как и (67 яблок) и (67 утюгов)
3) Сравнивать с собой? Запросто. Приведите цитату математиков, в которой бы запрещалось бы это делать.
Да вы сами ее привели выше:
Еще раз обращаю внимание на слово "бинарное".
Бинарное - потому что возвращает одно из двух: либо True, либо False
Сравнивается же тоже ... либо (Х = Х) либо (Х = not X), где Х - что угодно.
Я вам уже напоминал, что
а совсем не потому, что возвращает одно из двух.
И я вам писал, что принимает один или два аргумента, возвращает один из двух: только либо False, либо True (булев тип)
Такое ограничение на тип входных аргументов это не распространяется. Иначе говоря этими аргументами могут быть строки, числа, булевы значения
Что эта операция возвращает, не имеет никакого отношения к тому, как она называется. Только количество операндов.
Как тогда из множества {66,67,68} получились множества {66,67},{67,68},{66,66},{67,67},{68,68}?
У вас 67 - это элемент. И он может входить в различные множества.
Множеств, содержащих 67, может быть много. Элемент же 67 - один и тот же
P.S.
Так математики не пишут. В каждом из этих множеств по одному элементу
Вот до чего вас довело упорство в споре. Пишут, и не только так, но и
1 1 1 1 1 1
1 1 1 1 1 0
1 1 1 1 0 0
1 1 1 0 0 0
1 1 0 0 0 0
Цитату приведите из математики.
Множество {1, 1} - это множество {1}
А это цитата из математики. А вот Множество {1, 1} - это не множество {1}. Хотя бы потому, что у них разные свойства.
Вы меня извините, но это откровенная глупость. Ссылку дайте.
print({1, 1} == {1}) #True
Я понимаю, что мы примеры берем один из программирования, другой из алгебры, но корень разногласий нужно найти. Если каждый хочет остаться в своей области, то он прекрасно там себя будет чувствовать. Но мы-то хотим из них выйти в общее пространство. Поэтому я вас попрошу не просто написать print({1, 1} == {1}) #True, а сравнить написанное с {1, 1} == {1} = False.
Я вам уже сказал. То, что вы читаете как математику, к математике отношения не имеет. Ссылка где?
Так будет правильно?: {67},{67},{67}...
И эти множества существуют? Как и множество этих множеств?
Собственно я не против, будем множить не элементы, а сами множества!
Это одно и то же множество.
Множества {67, 68} и {67, 66} - разные
Да что вы на числах зациклились? Что, других равных объектов не найдем, что ли? Давайте рассуждать танками. Вот на полигоне выстроились 20 танков. Два танка абсолютно одинаковы (надеюсь, вы царапины не будете учитывать?). Так эти два танка - один танк? А двадцать - тоже один?
Точка с координатами (3, 4) - не то же, что точка(3, 5). И обе они - не то же самое, что точка. Это три разных сущности.
P.S. Вы располагаете танки в разных местах, т.е. каждый ваш танк имеет еще отличную от всех других расположение. Поэтому сущность (танк слева) - не то же (танк справа), хотя (быть танком) в этих танках одно и то же
Спасибо за дискуссию. Нужно бежать на работу.
Хорошо, в множестве М={a,b,c} существуют а,b и с. Но кроме них ничего нет? Откуда возьмётся некое d, которое не принадлежит множеству М, но при этом оно существует, так как (d=d) - истина. То есть Вы дали право на существование не только множеству М, но и не М?! Был тут некто Григорий, так он прямо от имени всемогущего призывал выпустить на волю всю адскую нечисть... Но это так, лирическое отступление. На самом деле, как мне кажется, необходимо учитывать кроме логики ещё и материал. Собственно к этому, насколько я понимаю, и призывает Спкус Халепний. Минус 20 на Севере это оттепель (при среднезимних минус 42), а плюс двадцать в какой-нибудь Африке может сойти и за похолодание.
d в М нет.
М={a,b,c}={a,b,c, NULL}={a,b,c,d l d={NULL}}
если вспомнить:
то not M=not {a,b,c,d l d={NULL}}={not a,not b,not c,not {d l d={NULL}}={a+1,b+1,c+1,1} и т.д и т.п... То есть если в любом множестве есть пустое множество, то это означает, что в это множество можно затолкать всё что угодно. А что угодно? По мне так угодно туда втиснуть бесконечность в виде континуальности! Представляете, весь математический Мир между нулём и единицей ( М=]0,1[ ) !
Это как понимать ваше: "Мое мнение: первично отношение"?
Возьмите теорию множеств. Пусть у меня есть множество F={a, b, c}. Первейшее положение, определяющая множество, что а "принадлежит" F или кратко: а Є F . (http://ru.eduarea.com/course/edu1a01d/view/Множества/Понятие_множества)
"Принадлежит" - отношение; a, b, c - "атомарность"... Как их разорвать?
И что тут главнее или первичнее? Как по мне это бессмысленно обсуждать в силу императива: ("Эйдос есть смысл", Лосев). Именно через эйдос (знают о нем или нет - безразлично) эти положения теории множеств имеют смысл (для философов)...
Единственно, что (я сделал) это свести и "атомарность" и "отношение" к единой двойственной субстанциальности, которая и соединяет их осмысленно...
Очень в этом сомневаюсь... Поскольку ваше: (существует, не) - это оппозиция ("анти-"), а в конструктивности целого, того же числа, необходим "орто-"-принцип... В неявном виде вы его и применяете, когда рассуждаете о функциях... Так нечестно !
!
"Эйдос и теория множеств"
ИМХО!!!
Можно ли мыслить элемент а отдельно от множества? Разумеется. … Также, как и можно отдельно мыслить Х отдельно от Y=F(X).
Если собирается некое целое из частей, то целое немыслимо без хотя одной из своей части. Но сама по себе часть этого целого вполне мыслима независимо (первичнее) от целого.
Это мнение Лосева. Не мое.
Сомневайтесь. Когда доказывается так это или нет, достаточно привести код, умеющий считать и не использующий в явном виде числа (0, 1, 2 и т.д), т.е. не использующий встроенные возможности компьютера к счету. Вы такой код можете привести? Критерий ведь прост: он должен работать
--------------- Вот пример кода --------------------------------
def null_or_one(lst):
#возвращает сколько элементов в списке
#умеет считать в пределах 0-1,
#не используя числа в явном виде
#lst - список чего-либо
count = "null"
for X in lst:
if X == X: #т.е. если Х истинно
count = "odin"
print('count = ', count)
return count
#1 пример: сколько элементов в ['a']?
#ответ: odin
null_or_one(['a'])
#2 пример: сколько элементов в []?
#ответ: null
null_or_one([])
Это как? Кажется у Аристотеля есть что-то на этот счет в его "Метафизике"... Вот палец руки - он часть этой руки. И он, по-вашему мыслим отдельно от руки и тела? - Странновато как-то... и жутковато даже...
***
Насчет построение числа...
Знаете, ваше доказательство машинное - это чистой воды жульничество... Ведь вы в программе используете эйдетическую логику:
идентификация (X) - эквивалентность (==) - логический выбор (if) - структуризация (count = "odin") - композиция
вот в этом месте:
Кроме того, вот это вы называете считать - // #умеет считать в пределах 0-1//???
Могли бы 0 и 1 заменить булевскими константами... Какая разница?
Нет уж! Возьмите просто исходно свою предикацию существования и ее отрицание и посчитайте! И снова - сомневаюсь...
А так, в вашем подходе, я не вижу ничего философского ... Нельзя же распространение электромагнитных волн объяснять наличием мобильника...
"Эйдос числа"
ИМХО!!!
Где ссылка на программу, которая умела бы считать, не используя при этом переменные типа int и не используя + …? Где, я вас спрашиваю?
Тут вы верно подметили. Но я утверждал и утверждаю, что нет никакой разницы между False и нулем, между True и единицей.
Вернее сказать: (X не существует) = (Х не-равно Х) = (ноль Х), (Х существует) = (Х равно Х) = (один Х). … Что касается именно такой записи, то где в терминологии эйдетической именно эти формулы приводятся? Cсылку предъявите.
Нет у меня такой ссылки! Она мне просто не нужна в онтологии, в ее конструктивной бессмысленности (о том и речь)! - Сдаюсь!
Бессмысленное - не считает.
Так в этом и весь смысл? Это похоже на самое гениальное музыкальное произведение, типа выходит музыкант, заносит пальцы над клавишами и 4 с копейками минуты абсолютной тишины, затем под бурные аплодисменты зала гений покидает сцену. Один квадрат Малевича чего стоит... И таких примеров тьма, вплоть до эзотерических связистов с космосом. Собственно вывод на экране монитора (в пиксели) ни в каких вычислениях вообще не нуждается, две операции прочитать и записать. Так я об этом и трындю уже который год, о времени чтения/записи, даже сравнивать ничего не надо, вещество заполняет пространство вдоль силовых линий Информационного Поля, это естественное состояние мироздания, человек с его логикой и прочими потугами как с боку бантик, в честь этого я и понизил всё человечество до уровня вещества.
Давайте без художественных сравнений!
Алгоритм какой? ... Мне известно только два подхода: аксиомы Пеано и Фреге-Рассела. В аксиомах Пеано говорится, что единица является натуральным числом, но она не выражается никои образом! Нет же определения. Что касается подхода Фреге-Рассела, то считать вложенные множества? Каким образом этот подход связывает выводимый ряд чисел с тем, что считаем?
Оперировать понятиями (равно, не), получая из этих примитивов более сложные конструкции, куда целесобразнее и практичнее!
0 - (ноль Х) = (Х не-равно Х)
1 - (один Х) = (Х равно Х)
2- (второй Х) = (один Х), что различается с каждым предыдущим.
3- (третий Х) = (один Х), что различается с каждым предыдущим.
Возьмите, например, множество {a, b, c}. Выберите элемент этого множества, например, элемент b. Можно ли о нем сказать, что b=b? Да. Тогда это будет первый элемент. Выберите из множества другой элемент. Он тоже имеет свойство быть равным себе: c=c или а=а выполняется? Да. Но проверить на равенство с собой мало, надо еще проверить на различие с предыдущими. Проверяем: (c не-равно b)? Да. Оба условия (равно с собой, различие с предыдущими) выполнимы. Переходим с следующему, т.е. отличному от выбранных, к элементу а.
По сути, когда рассматривается множество, то под элементами множества понимается только то, что они попарно различаются. У них нет иных свойств, кроме свойств различаться друг с другом! Вот их и используем, наряду со свойством каждого из них равняться себе!
Да не в этом дело. Вот Вы спрашиваете:
А приводите в пример код на языке высокого уровня. Вот и спрашивается, а как реализовано сравнение в машинных кодах, или хотя бы на ассемблере? Есть там а минус b? Или инверсия со сложением? Что то мне подсказывает, что там кроме прочитать и записать ничего нет! А всё, что принято называть логикой скрыто в железноскроенные комбинационные схемы. Там даже компилятор не то что бы не Бог, им там и не пахнет!
run_nr_i ... ссылка кода [c 17], ссылка видео
=, not ... там есть и этого достаточно.
Вот и дом - это не то же, что кирпич, а их совокупность, выложенная по определенным правилам.
Интересные статьи, спасибо. Правда пока только пролистал, потребуется время на чтение/запись :) . Вот такой вопрос, а могли бы вы пересказать весь текст не используя картинки, обозначения, формулы и коды, и даже числа/цифры, то есть что бы в тексте были только слова, ну ещё точки с запятыми? Я как то экспериментировал таким образом, сначала было трудно, представьте, как в словах передать схему телевизора?, так и хотелось схватить карандаш и нарисовать, но потом начал привыкать, оказывается русский язык достаточно самодостаточен. Для чего мне это было нужно? По работе частенько приходится чинить/вводить в эксплуатацию технику по телефону. По этому такие эксперименты мне очень помогли. Признаюсь честно, я и ФШ эксплуатирую в том же духе, помню как меня заклинило, когда в классе восьмом-девятом впервые пришлось говорить по телефону...
Что произойдёт, когда в компе батарейка сядет? В первую очередь слетит дата и время, и уже только этого достаточно, что бы операционная система загнулась. Откуда комп возьмёт время? Он его не помнит, и не вспомнит без внешнего вмешательства. То есть создаётся впечатление, что времени вроде бы нет, но при этом без времени всё рушится! Где в Вашей логике время? Одних кирпичей и правил недостаточно, требуется ещё и последовательность. Может быть существовать означает существовать во времени? Пока часы идут, дом есть, как только остановились, так и дом исчез, разрушился, как та самая операционная система. Правда в таком случае без абсолютного хронометра не обойтись.
Нигде.
Я же приводил логику:
a - то же, что различается с b,c
b - то же, что различается с a,c
c - то же, что различается с a,b
Других формулировок для элемента множества нет! Но еще каждый из них равен себе, т.е. существует. Иначе говоря, при конструировании чисел натурального ряда ... используется только ... равно, не ... в различных комбинациях.
Ну с цифрами и буквами я бы ещё согласился, поскольку в операционной системе есть кодовая таблица (та же ASCII), а вот с числом нет, не получится сравнить 21 и 22 без арифметических операций, без конвертации с помощью того же int (или char по умолчанию). Другими словами 21 это
1111111111
1111111111
1000000000
0000000000
0000000000
0000000000
0000000000
0000000000
0000000000
0000000000
, или 15 в шестнадцатиричном виде. Другими словами ряд натуральных чисел с помощью =, не не конструируется, здесь потребуется рекурсия, что бы этот ряд упорядочить по возрастанию, иначе как туда запихать "дурную бесконечность"?
А как быть со знакоместом? Это же упорядоченная последовательность. Или я ошибаюсь? Тогда абсолютным хронометром будет "маленький" фонарик - генератор тактовых импульсов.
Суть же в другом! Так, 3-й не-равен 2-ому потому, что хотя 3-й равен себе, как и 2-й ... но ... 3-й различается с 0,1,2 ... а 2-й только с 0,1 ....
Его нет в булевой алгебре. И у меня его нет.
Собственно, вы пользуетесь интеллектуальным механизмом различия и тождества, изложенным А.Ф. Лосевым в "Самое Само":
различие - тождество - становление - ставшее - проявление ,
формализуемое как "противоречие", через примитив А=А. Какой смысл?
***
Прочитал вашу книгу. Мы по разные стороны "баррикад". Я это маниакальное и противоестественное А=А не приемлю... ( "Эйдос. Первый закон логики"). Нет его в онтологии... . Оно нужно только тому, кто хочет найти противоречия на пустом месте... Собственно это гегелевский некротический подход... На здоровье!
Самое интересное, что вы используете функции (когда вам надо), в которых никаких противоречий нет, поскольку они представляют собой эйдос ( "Эйдос и теория множеств"):
операциональность - переменная - операция - функция - композиция функций
***
Я снова возвращаюсь к лосевскому: "Эйдос есть смысл".
Эйдетическое число несет в себе интеллект. А точнее (согласно представлениям Платона об интеллигибельном) является неким интеллектуальным усилителем на оси "одно" - "многое". Где "одно" - унифицированная единица, а "многое" - необходимая структуризация.
Природа применила этот механизм "унифицированной единицы" для создания (структурирования) организма. Например для нейронной сети в мозгу. Мы только повторяем эти механизмы: из магазина - сеть магазина; из компьютера - сеть компьютеров, из деталей - двигатель, ...
Вот вы правильно пишите:
Но с философской точки зрения (предельного обобщения) кирпич - унифицированная единица ("одно"), а дом - необходимая структурность ("многое").
У Платона было несколько иное (в отличии от вас) представление о существовании ("Софист"):
Ваше привести не могу, оно в формате картинки на стр. 5. Мне ваше представление не подходит... (простите!)
Согласно его представлению об интеллектуальном, в свете существования эйдосов, он-то и является предельной (конвергентной) организационной унифицированной единицей для всего сущего (пять видов сущего). Где во втором статусе любого эйдоса и появляется сущность - унифицированная единица.
И ваша финишная строка в вашей книге:
Она возможно только благодаря эйдосу, который поддерживает единый формат интеллекта в "деревьях" ("Эйдос и интеллект") и т.п.
***
Собственно сущее потому некое "одно", что оно транслирует через себя механизм самоподобия. Мы потому и можем работать с функциями и функционалами, что они в едином эйдетическом "формате" числа. на этом же "формате" (интеллекта) построен наш язык... Собственно тупик философии (как я ее вижу) - это непонимание Платона и его мира интеллигибельного... Эволюция требует ответственности от субъектности. Вот в "Софист" он попытался это обосновать... Но наш мир "людей" эгоцентричен - каждый пытается внедрить свое, не замечая как бы проделанное... Это не честно ! Возможно (не хотелось бы) и я что-то недопонимаю...
! Возможно (не хотелось бы) и я что-то недопонимаю...
***
Владимир! Я могу и ошибаться, но ваши отношения с нулем как противоречием мне представляются напрасными. Нуль - это семиотический знак границы. Отсюда логично - 10, 100, 1000... Вы же:
Кстати сказать, самые большие трудности философского плана проявляются именно с семиотикой ("Античность. Аристотель. «Целое больше суммы своих частей»" ). В этой части, методически, у вас алгебра Буля с ее символизмом появилась раньше сущего...
Типичная ошибка философов, они часто в свое описание запускают себя как актора-творца. У меня не так. У меня акторы (пассивное и активное) субстанции (причина самого себя). Я только проверяю их как сущее - на принцип самоподобия, поскольку я его (сущего) "представитель" как Homo...
Так, как пример, согласно Бартини и П.Кузнецову двойственность мира может быть выражена как [L, T]. В таком представлении L - "прошлое", T - "будущее" (смотрите таблицу в «Эйдос. Субстанции пассивности и активности»), а настоящего в имманентном нет! Настоящее появляется исключительно через эйдос как лосевское становление... В настоящем расположена субъектность как осцилляция...
***
Спасибо за дискурс. Извините если что-то не так. Но между нами "баррикады" ...
Программы, использующие это:
- работают, получают верный результат. И это главное.
Гегель начинает с чистого небытия, я тоже. Не-быть = (не-быть = быть).
Это кибернетика. Прочти "Введение в кибернетику" Р. Эшби
Да, мое мировзрение - это философия Лосева и Гегеля, кибернетика Эшби и Турчина
Как быть с бесконечностью? Ккуда девать Кантора с его инфинитами? Ведь ноль ведёт себя так же как и бесконечность, ноль плюс ноль равно ноль, бесконечность плюс бесконечность равно бесконечность (осталось договориться о том, что нечто поделить на бесконечность равно ноль, нечто поделить на ноль равно бесконечность). И ещё раз обращаю Ваше внимание, операции "сравнение" (как и отрицание) в Булевой алгебре нет, есть только инверсия.
Принт-скрин из "Математическая логика" Колмогорова
Что же тут поделаешь, "если доктор сказал в морг, значит в морг", хотя я против : vlopuhin, 25 Июль, 2016 - 12:00, ссылка.
Что такое пустое множество? Пустое множество - это множество, не содержащее ни одного элемента. Другими словами, пустое множество - это множество, в котором нет элементов. Как это выразить формулой?
Только так: каждый элемент такого множества не равен себе.
Замечу здесь, что в формуле (Х не-равно Х), если вместо Х подставить само множество, то получим парадокс Рассела, т.е. получим такое множество, которое не существует.
Формула противоречия: (X не-равно Х), что в более подробном рассмотрении означает (Х не-равно Х) тогда, когда (Х равно Х)
Поскольку
нет Х = (Х не-равно Х)
нет Х = Х - Х
то
Х -Х = (Х не-равно Х)
Да, Вы сформулировали парадокс Рассела и дали определение пустого множества. Но вопрос в том, разрешим ли парадокс Рассела в рамках конкретного языка, и сколько пустых множеств, одно или сколько захочешь? Если парадокс разрешается, то это уже не парадокс (а он разрешается в программировании, так как научили комп независать, даже переполнение памяти частично/временнно победили). Если пустое множество одно, то откуда плодятся нули перед первой значащей цифрой?
Не разрешим.
Что значит не разрешим? То и значит, что не имеет решения. Формула (X не-равно Х) не имеет решения, она всегда возвращает False.
Разве возвращение False не есть разрешение? При сравнении выбрано истинное значение, другого просто не дано. Как Вы интерпретируете ответ компьютеру по барабану. То есть парадокс возникает уже на стадии есть/нет, если парадокса нет, то и разрешать нечего.
Почему на ноль делить нельзя? Потому что получаем (Х = не-Х), т.е False
5/0=X
X*0=5
Так при каком Х получим равенство? Ни при каком
Такие записи находятся за пределами истинности (False)
Как Вы получили вот это?:
Насколько я понимаю, вот так: (5/0=Х) ->(0*(5/0)=0*(Х))->(5=0*Х)
На втором шаге Вы ноль на что умножали? Компилятор пропустит такой код?
Так: http://elementy.ru/email/1530320/Pochemu_nelzya_delit_na_nol
А не математики? Вычитания нет по другой причине. Допустим у Вас червонец, Вы покупаете трёх раков по трёшке. Продавцу и в голову не придёт отнимать от десяти один, он даёт Вам трёх раков по трёшке и добавляет рубль для равновесия. И умножения нет, поскольку это последовательное сложение. А вот деление есть, и вопрос остаётся в силе:
Речь о математике, а не о вложенных правилах математики на компьютере
print(4/0 == 5) #ZeroDivisionError
print(4 == 5*0) #False
Таким образом парадокса нет просто по определению, просто по тому, что так решил великий компилятор, а не по тому что он разрешен!
Вспомнилось из КВН.
По-моему, из Казани (могу ошибаться) : "татары не отступают, они разворачиваются. И вперед!"
P.S. Избегать решения (Х не-равно Х) - не тоже, что найти решение (истинное) этой формулы.
Компилятор мог и (Х не-равно Х) принять за ошибку. Так что, как говорят врачи, это не Вы здоровы, это мы недоглядели.
Между прочим, ошибка - это и есть ложь (False) . Он просто сообщает, что при делении на ноль имеем False типа ZeroDivisionError
Это можно перевести так: парадокс есть, но разрешать мы его не будем, не царское это дело, обставим флажками и пойдём дальше. В принципе можно и так, мало ли чего в мире есть/нет, потом изобретём хитровымудренную лопату, вернёмся да раскопаем. Или так. Был у меня в отделе парень, он изрядно помучившись приезжал с объекта и говорил: там ошибка типа ZeroDivisionError нужно вызывать сервисного инженера! А ты кто говорю я ему?...
Скажу иначе, сравнив:
1) Гегель (наука логики) : ничто есть, стало быть, то же определение или, вернее, то же отсутствие определений и, значит, вообще то же, что и чистое бытие.
2) Эквивалентность в мат. логике: 0 = 0 ~ 1
+++++++++++++++++++
3) нет-быть = не-быть ~ быть
4) Без противоречия (без тождественно ложной формулы) нельзя выразить нечто полным образом, поскольку необходима не только истина, но и ложь.
Думаю физики (да и философы) с Вами не согласятся. Пустоты нет. Мир непрерывен, по тому и аналитичен, то есть познаваем.
Ноль как таковой - не то же самое, что ноль в позиции определенного разряда.
Также как нельзя приравнивать, например, собаку и собаку лайку
P.S. Если нет собаки-лайки, то это не означает, что нет и собаки. Но если нет собаки, то это означает, что нет и собаки-лайки.
То есть Вы как фокусник вытащили из шляпы голубя (где там в глубине памяти теплилась надежда на то, что в запасе есть знакоместо). А что делать когда и эти места закончатся?
В чем проблема? Нет никакой проблемы. Для {} имеем множество элементов, таких как (А не-равно А), (В не-равно В),(С не-равно С), ... т.е не-быть чего (этих А В С) может быть хоть сколько
Нет, хоть сколько не получится, либо 32, либо 64, дальше придётся "изобретать велосипед".
???
Воспроизведу одну цитату из И. Бродского ("Сталинизм - это прежде всего система мышления и только потом технология власти")
Откуда возникает Двоемыслие? Как теряются нравственные критерии? Зачем Гегелю нужна была спекулятивная логика (Ничто), вопреки онтологии? Зачем "интеллигенции" СССР нужен был Гегель? А как же быть с "тождеством бытия и мышления" Парменида? Движет ли искусственная формализация (типа: А=А и А не равна А) науку к Истине (учитывая, что тут мы "включаем" искусственную алгебру Буля)?
Я не знаю Истину на это и вынужден полагаться на интуицию. При этом, учитывая, что философия предел конвергенции, задумываясь над разными планами Бытия, в том числе и историческими... Это так - размышляю над дискурсом..
ИМХО!!!
Р.S/
Кстати! Для себя я уяснил, что из алгебры Буля эйдетической (программной) логики не получить, а наоборот - элементарно! "Мышление (эйдетический логико-философский аспект)" , приложение {5}.
Ровно по той же причине, почему каждая селедка - рыба, но не каждая рыба - селедка.
Ровно по той же причине, почему точка с координатами, например (3,4) - не тоже, что точка.
Цитата из [Философия логического атомизма, Б. Рассел]:
“Если бы случилось так, что греков не было, то и пропозиция 'Все греки являются людьми', и пропозиция 'Ни один грек не является человеком' были бы истинными. ...
Пропозиция 'Ни один грек не является человеком' - это, конечно же, пропозиция 'Все греки не являются людьми'. Если бы случилось так, что греков не было, обе пропозиции были бы истинными одновременно”.
Кратко запишем то, что изложено Расселом:
1. Греки – не существуют.
2. (Все) греки – люди.
3. (Ни один грек – не человек) = (все греки – не люди)
4. Для (Греки – не существуют)
Истинно как (все греки - люди), так и (все греки – не люди)
Комментарий к сказанному Расселом:
5. Рассел отвергает такую конструкцию, поскольку она противоречива, поскольку такая конструкция (все греки - люди)= (все греки – не люди) всегда ложна, т.е. всегда False.
6. Но что есть пустое множество? Пустое множество – это множество, в котором не существует элементов и выражено оно именно как {Х | X не-равно Х}, т.е. это множество, в котором каждый элемент не равен себе. Эта формула (Х не-равно Х) всегда ложна. Согласно же определению самой математики, формула, которая всегда ложна, является ПРОТИВОРЕЧИЕМ!. … Ссылка на понятие пустого множества { Х | X не-равно Х }: [Математическая логика, Колмогоров, с-130]
Если истинно (все греки - люди), то не может быть, чтобы истинно было так же (все греки – не люди). И наоборот.
Иначе говоря, не может быть, чтобы (все греки - люди) и (все греки – не люди) ... было бы одним и тем же, тем же самым (=).
Но если стоит задача выразить именно это "не может быть", т.е. выразить "не существование", то нет иного способа как сказать {Х | Х не-равно Х}, что и указано Колмогоровым!
Далее Рассел пишет:
Комментарий:
Когда речь идет о не существовании чего-либо ... нам и нужна ошибка, т.е. False!
ОТРИЦАНИЕ КАК ЛОГИЧЕСКАЯ КАТЕГОРИЯ / БОНДАРЕНКО
Стр-8
1) саисарга — абхава, означающее отсутствие чего- либо в чем-то другом (форма суждения «S есть не в Р»),
2) апьйопъя — абхава, означающее то, что одна вещь не является другой вещью, т. е. отличие одной вещи от другой (форма суждения «S не есть Р»),
Комментарий:
1. (стол есть not стол) сводимо как к (стол не-есть стол), так и к (not стол не-есть not стол).
2. (стол не-есть not стол) сводимо как к (стол есть стол), так и к (not стол есть not стол).
Стр-14. Замечания Аристотеля в «Метафизике» также свидетельствуют о том, что утверждение и отрицание понимались им как полагание мыслимого существующим или несуществующим.
Утверждать — значит говорить, что данный предмет (или признак) существует;
отрицать — значит говорить, что данный предмет (или признак) не существует, т. е. не имеет места в действительности.
Комментарий:
БЫТЬ: (Стол есть стол) т.е. стол существует как стол. (Стол не-есть not стол) т.е. стол не существует как not стол.
НЕ-БЫТЬ: (Стол не-есть стол) т.е. стол не существует как стол.
Стр-16
Как видим, небытие (несуществование) понимается Аристотелем как лишенность, или отсутствие («отрицание того, что отрицается, есть его отсутствие» [Аристотель 1976, 121]). Понятие лишенности (отсутствия) связано с понятием различия («инаковости»), ибо лишенность есть в каждой паре противоположностей (например, зрячий—незрячий и т. п.). А противоположность — наибольшее различие в пределах рода, «противоположность есть некоторого рода различие, а различие есть инаковость». Основная противоположность — наличие у вещи того или иного свойства и отсутствие его (т. е. обладание и лишенность) [там же, 121, 235, 262, 236]. Стало быть, отрицание — одна из форм противопоставления («противолежания»), ср. зрячий (обладание) — слепой, или не зрячий (лишенность). Противоположные (противолежащие) друг другу утверждение и отрицание (например, Он сидит и Он не сидит) Аристотель называет противоречием, одни член которого всегда необходимо истинный, а дру гой — ложный [Аристотель 1978, 84, 97]. Эта противоречивая противоположность (как, впрочем, и остальные три «противолежания») рассматривается Аристотелем как различие. Таким образом, понятие отрицания как выражения несуществования (небытия) раскрывается Аристотелем через понятая отсутствия, лишенности, различия, противоположности.
Комментарий:
Для выражения не существования … необходимо не только отрицание, … но наличие противоположностей в одном.
Стр-17
Изложенное позволяет сделать вывод: утверждение и отрицание в концепции Аристотеля интерпретируются как полагание в мысли чего-то в качестве существующего или несуществующего (т. е. истинного или ложного), присущего или не присущего предмету мысли в действительности.
Комментарий:
(Х равно Х) – истинно. … {Х | Х равно Х} не-пустое множество
(Х не-равно Х) – ложно … {Х | Х не-равно Х} пустое множество
Х – Х = (Х не-равно Х)
т.е. минус = не-равно
Рассмотрим ряд: -3 -2 -1 0 1 2 3
3 – 3 = (3 не-равно 3), 2 – 2 = (2 не-равно 2), 1 – 1 = (1 не-равно 1), 0 – 0 = (0 не-равно 0)
По экспериментируем, например:
3 +(–3) = (3 не-равно 3) так: 3 = (3 не-равно 3) + 3
Подставим, используя “минус = не-равно”: 3 = (3 - 3) + 3
Получим 3=3.
Выводы:
Далее сравниваем:
(1 = 0 + 1) и (1 = not 0)
Получим:
not = +1
Именно используя это (отрицание по отношению к предыдущим числам) программа run_nr_i конструирует числа натурального ряда, не используя явно +1.
Как известно: 1 = +1, -0 = 0 = +0
Тогда: (not (not 0)) = 2
Поскольку: (not 0) = +1 +0 = +1 = 1, (not 1) = (+1 +1) = 2
Соответственно: not (Х не-равно Х) = (Х равно Х). Следовательно: not (нет Х) = есть Х, not (ноль Х) = один Х.
Поэтому формула (not (not 0)) = 2 может принять вид: (not (not (Х не-равно Х))) = 2 Х
Сравнение конструирования чисел натурального ряда с теоретико-множественным определением Фреге-Рассела
1 = {0} = {{}} ... 1 = (not 0)
2 = {0, 1} = {{}, {{}}} ... 2 = (not (not 0))
3 = {0, 1, 2} = {{}, {{}} , {{}, {{}}} } ... 3 = (not (not (not 0)))
Те числа, которым нас учили в школе, применяя счеты, формируются при помощи "квадрата" (горизонтали и вертикали):
один, два, три, .... десять
одиннадцать, двенадцать, .... двадцать
двадцать один, двадцать два, .... тридцать
....
восемьдесят один, восемьдесят два, .... девяносто
девяносто один, девяносто два, .... сто
Это и называется в эйдосе числа - группировки:
полагание - единица - ряд - группировки (разряда) - представление
Ясно, что такой статус имеет в 4-м статусе гомологию с другими эйдосами (плоская фигура в геометрии или энергия в физике и т.п.)
Или даже с тем же эйдосом арифметических операций:
непрерывность - дискрет - сложение - умножение - возведение в степень
отсюда, естественно (гомологично) появляется "квадрат" таблицы умножения...
А ряд по принципу:
это нечто иное, о чем я и писал в "Эйдос и теория множеств":
Я к тому, что мы в своей культуре пользуемся исключительно эйдосами (единый формат интеллекта), а не "теоретико-множественными" построениями... Мне так кажется...
В теоретико-множественном построении отсутствует что мы считаем. Я не представляю, каким образом можно, используя этот подход, решать простые задачки первого (и далее) класса.
Вы противоречите (not ) практике жизни!
) практике жизни!
ИМХО!!!
Какой, блин, практике? Пишите аргументировано.
Пусть на елке никто не сидел. Прилетела синичка. Сколько птичек на елке?
Теперь переведите это на определение единицы Фреге-Рассела, т.е. на 1={{}}
Простите, Владимир!
Но я исчерпал свои аргументы!
Мои аргументы просты:
1 птичка = (not (птичка не-равно птичка))
1 птичка = (птичка равно птичка)
1 птичка = +1 +0 птичка
Ну, я же и говорю, я не знаю как в первом классе объяснить детям ваше not? Не знаю!!! А если честно - не вижу в этом смысла! Я же сразу честно сказал - "баррикады"...
Удачи!
Дети, у нас ничего нет. Когда ничего нет, то это ноль. Тогда что будет если мы мы скажем не ничего? Верно, что-то. Например, у нас не было яблока. Что будет, если мы скажем (не (не яблоко))? Яблоко. Яблоко остается тем же самым яблоком, оно же не изменяется в грушу или червячка? Нет. Так вот, когда мы о чем-то говорим, что (яблоко остается тем же самым яблоком), то мы говорим, что это (яблоко - одно)
Аксимы Пеано (иногда начинают с 0, в этой формулировке с 1)
1) В N существует натуральное число 1, называемое единицей;
2) За каждым натуральным числом n непосредственно следует однозначно определенное натуральное число n’, называемое следующим за числом n;
Замечание: далее всюду число, следующее за натуральным числом n, будем обозначать символом n’.
3) 1 (единица) не следует ни за каким натуральным числом, то есть не существует такого натурального числа n, что n’ = 1;
4) Если некоторое натуральное число n’ следует сразу за числом n, а также следует сразу за числом m, то числа n и m тождественно равны;
5) Пусть какое-нибудь утверждение верно для 1 (единицы). Тогда, если мы предположим, что это утверждение верно для некоторого натурального числа n, и из этого предположения получим, что оно верно и для следующего за n натурального числа, то мы сможем заключить, что наше утверждение верно для любого натурального числа.
Комментарий:
Что значит следует в (За каждым натуральным числом n непосредственно следует однозначно определенное натуральное число n’, называемое следующим за числом n)?
То и значит, что различаться с предыдущими, что и выражено как not в сравнении с каждым предыдущим, т.е. (+1 = not)
По моему всё таки здесь речь идёт не о числах, а знакоместах. Иначе откуда берутся четные числа, простые числа?
Что следует из not 5? Почему 6? Может быть всё что угодно, кроме 5?
Какие могут быть утверждения о единице, кроме того, что это число?
Мы конструируем числа. Поэтому (изначально) нет чисел. Вообще нет! Тогда:
1 - это то, что NOT каждое предыдущее.
Предыдущее что? Ноль. Тогда, по определению, пусть это (не ноль) будет число п7н
2. - это то, что NOT каждое предыдущее.
Предыдущее что? (Ноль, п7н) Тогда, по определению, пусть это (не ноль и не п7н) будет число е5ok
Получен натуральный ряд: ноль, п7н, е5ok.
т.е
ноль +п7н = п7н,
п7н +п7н = е5ok.
Я на этот вопрос почти в каждой теме пишу:
1 - это равняться себе. ... Пусть имеется {a, b, c} Почему о каждом элементе этого множества можно сказать, что оно одно? Потому что (а) равно себе, потому что (b) равно себе, потому что (с) равно себе, т.е.
1 а ... поскольку а=а
1 b ... поскольку b=b
1 c ... поскольку с=с
Да, получен натуральный ряд, но ряд всего чего угодно, но только не чисел. Вот я и предположил, что получили место в натуральном ряду. Любое число само по себе должно иметь какое то свойство, по которому его можно затолкать в ряд натуральных чисел в строго отведённое для него место. Откуда это свойство (или атрибут?) появляется в числе?
Дело не в названии чисел натурального ряда. В Росии - это один, два, три. У англичан - это уан, тю, фри. В Эстонии - это юкс, какс, колм.
Так что такое это (один, уан, юкс)?
один, уан, юкс - это NOT предыдущее. Где этим предыдущим является НЕРАВНОЕ СЕБЕ
В данном случае дело именно в названии, то, что назвали числами, они и в Африке это самое и есть, правда обозначаются трошки иначе. Дело в том, что в ряд натуральных чисел как то затесалось упорядочивание по возрастанию, получается это главное отличие ряда натуральных чисел от просто множеств. Благодаря этому именно в ряде натуральных чисел появляется потенциальная бесконечность, больше её нигде нет!
Зачем лезть в бесконечность, если с нулем и единицей трудности в понимании? Ряд натуральных чисел конструируется по возрастанию, т.е. +1. Но что значит это +1? То и значит, что отрицая каждое предыдущее число, где изначальным числом является нет-быть.
1 = 0 + 1
1 = not 0
Не понятно, где здесь +1? Без потенциальной бесконечности ноль так и останется пустым множеством, и никогда не станет числом. А без этого как Вы собираетесь объяснять мне-первокласснику что такое отрицательные числа?
1 = 0 + 1 = +1 +0 = not +0 = not 0
1 = not 0
Кажется я начинаю понимать! Ведь это всё навороты методики преподавания математики? Я не помню, как я научился считать, по моему я это умел всегда (отец однажды мне как рассказал что к чему), хотя некоторые воспоминания есть, труднее всего было запомнить название цифр и некоторых чисел (десятки, сотни, и ещё эти одиннадцать, двенадцать ...), то есть это нужно было просто зазубрить/запомнить, но а дальше как по маслу, просто считать, не палочки и птичек а просто считать (придя в первый класс я уже уверенно считал до тысячи, можно было и дальше по аналогии, но я ещё не знал слова миллион). Отсюда вопрос, если просто считать это считать числа? Теперь у меня возникает сомнение, вот уж точно горе от ума...
Вот и мне всегда казалось странным, что понятия чисел (хотя бы нуля и единицы) никак не формулируется. Эти понятия поясняются на примерах, но не даются формулировки.
Более того, считать в пределах (0, 1, много) умеют даже животные.
Но если это так, то эти формулировки должны быть до банальности просты!
А ещё в компе слово и число ни чем не отличаются, для этого и требуется типизация. Именно такие рассуждения подталкивают на мысль о том, что проще информации ничего нет, это то основание на котором "растут грибы", то есть слова и числа (одного поля ягоды!).
Как работает мозг? Как работает его нейронная сеть? Как устроен отдельный нейрон?
Так и устроен, что он сравнивает с пороговым значением, т.е. принимает решения есть или нет ... на основании равно порогу или не равно порогу.
Хочу сказать, что возможности считать заложено в живом изначально, в силу его устройства на самом элементарном уровне.
Отсюда появляется деление систем на системы с отрицательной обратной связью (технические), с положительной обратной связью (живые), и без обратной связи (конверторы). Последние на мой взгляд самые интересные, на вход число, - на выходе смысл. Просто благодать! В общем информация это свет. А свет это спектр, отсюда и числа, и "вычислительные методы"!
А всё потому что кроме not есть ещё одна самая простая операция "пофиг" (или высокий импеданс). Это значит, что "быть или не быть" отходит на второй план, на первом "пить или не пить". Шутка конечно, но доля правды в этом есть, если существовать и не-существовать, то надо бы задуматься где?
Что понимается в математике, когда говорят, что выражение (формула) не имеет смысла? Когда результат сводится к запретному. Что это значит?
Самый распространенный пример - деление на ноль. Например, (5:0) - бессмысленно. Почему? Потому что это сокращенная запись от (0 * x = 5). Такого числа, которое при умножении на 0 даст что-то кроме нуля, просто НЕ СУЩЕСТВУЕТ. Левая часть равенства (0 * x = 5) НИКОГДА не равна правой части равенства. Поэтому сказать, что (0 * x = 5) бессмысленно - то же, что сказать, что (Х = not X) есть False, т.е эта формула всегда ложна.
Но так, используя ложь, формулируется пустое множество {X | X не-равно Х} [Математическая логика, Колмогоров, с-130] Почему? Потому что только так можно передать смысл НЕ СУЩЕСТВОВАНИЯ Кроме того, используя не только истину, но и ложь, строятся таблицы истинности. Так, при делении на ноль мы получаем ошибку типа ZeroDivisionError, т.е мы получаем False типа ZeroDivisionError. Всего лишь! Такая запись (0 * x = 5) говорит лишь о том, что она не истинна.
Резюме всего сказанного: для полноты выражения чего-либо нам нужна не только True, но и False! В противном случае, используя только истину, то, что не существует - невыразимо
В самом, если можно так выразиться в "чистом виде", ложь формулируется следующим образом: False = (False = True)
P,S. Что значит полнота выражения? То и значит, что нужно выразить либо истинно, либо ложно. Но ложь - это и есть (False=True), т.е. ложь - это (ложь и истина - одно)
Выражение может быть истинным или ложным в некоторой логической системе (например, в русском языке, которым я думаю). И раз уж речь зашла о смыслах, то лжи нет в том смысле, что обмануть самого себя невозможно, хотя незнание и не освобождает от ответственности.
Cмысл лжи, как говорят математики, в том, что из лжи следует как ложь, так и истина. Это прямое следствие формулы False=(False=True)
print(False==True) #всегда False
Из Вашей формулы следует две лжи, одна истина, и ещё два "равно" и две скобки. Скобки разные, одна правая, одна левая, а вот с "=" надо бы разобраться, по моему они тоже разные, первая читается как "из (False=True) следует False", а вторая как "False равно True", то есть "следует" не равно "равно", и это легко проверяется с помощью написанных Вами программ. Ну что тут скажешь, я просто герой, раскусил Ваш компилятор, он прозрачен как стекло, его легко можно обмануть, поскольку из лжи следует как ложь, так и истина. Оно и понятно, это же компьютер, что в него загрузишь, то он и схавает. Например, вместо 5/0=Х подсунем ему 5=0*Х, и дело пойдёт.
C ложью логика работает. Если 5=0*Х просто возвращает False, то 5/0 возвращает False типа ZeroDivisionError, которую можно заключить в обработчик ошибок try. Проблем никаких нет с точки зрения дальнейшего выполнения программы. В этом смысле исключение - не проблема.
Но с точки зрения математики, формула (Х = не-Х) - не решаема. Это означает, что она (эта формула) НЕ ИСТИННА - она ложна, причем всегда ложна.
И тут возникает мировоззренческий конфликт. Математика ищет истину, только истину. Но при этом не может обойтись без лжи.
В булевой алгебре формула False=(False=True) записывается несколько иначе False=(False~True), т.е. False - это эквивалентность лжи и истины.
В той же булевой алгебре свойства импликации: из лжи следует как ложь, так и истина.
В самой же формуле False=(False=True) это свойство импликации вытекает из того, что
1) (False=True) т.е ложь
2) False=False т.е. не-ложь
Что же тут поделать, работа у неё такая, выполнять заказ физики. А как на счет исключенного третьего? В смысле существуют такие вещи, которые не по зубам ни математике ни физике?
Исключение третьего: либо истинно, либо ложно (третьего не дано). Но сама ложь и будет тем третьим, поскольку она (ложь) есть равенство с истиной.
Можно ли это понимать так, что есть нечто (третье), и это нечто нельзя принять ни за ложь, ни за истину? Тогда почему Вы поторопились обозвать это нечто ложью? То есть компьютер может работать с одинаковым успехом как в положительной (0V,+1V), так и в отрицательной логике (-1V,0V), симметрия абсолютна, можно с одинаковым успехом плодить как истину, так и ложь. В этом плане вновь проявляется парадокс Рассела, или по другому вновь наружу лезет дурная бесконечность.
Прочтите из булевой алгебры (напишите словами): False = False ~ True
1. Ложно то, что ложь эквивалентна истине. (в этом утверждении две лжи, и одна истина)
2. Истинно то, что ложь не эквивалентна истине. (в этом утверждении две истины, и одна ложь)
По моему этот факт можно интерпретировать линейностью логики, в частности Булевой алгебры. Тогда возникает вопрос, что такое нелинейная логика? Вообще в природе такое встречается? Или это нечто нежизнеспособное, типа вариантов ДНК-кода множество (и это множество как ни крути конечно), но не все варианты совместимы с жизнью. Таким образом нелинейная логика обречена на вымирание? Ну так устроена жизнь!?
Вот и я так понимаю (ложь - то же, что ложь эквивалентна истине). ... Только почему утверждаете, что здесь две лжи? Потому что False по обе стороны равенства? ... Это же одна и та же ложь.
Вот что в математике нет, так это оператора присваивания. А он, между прочим, встречается гораздо чаще других, если речь идет о программировании. Почему?
Почему его нет в математике? Потому что если его интерпретировать как равенство, то получается явная ложь. Взять хотя бы пример со счетчиком : I = I + 1. Его левая часть никогда не будет равна правой.
Почему, напротив, в программировании он превалирует? Потому что "жизнь" заставляет описывать результаты изменения через равно. ... Было сначала I, затем изменилось и стало другим.
Хочу сказать, что там, где есть изменение, там ... никак без лжи, т.е. никак без перехода одной истины в другую.
В общем случае: было Х, стало не-Х. И если нет ничего третьего между этими Х и не-Х, то этим третьим как раз и является это ничего, т.е является (х = не-Х)
Да, именно так, я посчитал количество слов в предложении.
Спорное утверждение, кто же знает, как там всё устроено на самом деле, всякий раз приходится оперировать копией. Вот и здесь то же самое:
Так ведь его и в программировании нет в чистом виде. Я об этом и говорил выше, там сплошные прочитать/записать. Читаем I в первый регистр, читаем единицу во второй регистр, крутим ручку арифмометра и читаем результат в I. Вот это "крутим ручку арифмометра" можно принять за самое главное действие, вот там и просиходит вечное становление по Гегелю:
Там то как раз собака и порылась, оттуда вся хрень и лезет, и самый главный там генератор тактовых импульсов (пока главный архитектор отдыхает). Но вот проснулся главный архитектор и рубанул по фазе. Заглядываем внутрь, а там нет ничего такого, за что мог бы зацепиться пристальный взгляд художника...
Другими словами, в программировании ответ всегда известен из постановки задачи, там знак равно не нужен.
Что это, если не присвоение? Оно и есть. Берем переменную с каким-либо значением, например, регистр. Потом значение его изменяем.
В самом общем виде: X=F(X), где
F - какая-либо операция: например, суммирование с единицей; = это присвоение
Это и есть двунаправленный информационный поток! Психологи называют это "зрительный контакт". Физики "неустойчивое равновесие". Я это называю "капелька воды на раскалённой сковороде, смазанной маслом". В самом деле, старое Х ещё не исчезло, новое Х ещё не появилось, есть только F - "оператор Жизнь". Тогда F это не какая-либо операция, это целый пучок, другими словами целое информационное пространство, Единый, он же Реальность. Вот и из Вашего:
следует, что "F" и "=" одно и то же.
Думаю, что разные.
Хорошо, пусть будет F это преобразование, = это действие. Или F это восприятие, = это мышление (Бытие)?
Простите, что вмешался.
Логика в своей основе нелинейна. Линейно будет движение из одного состояния в другое, "по синусоиде". Но "по синусоиде" нет остановок. В максимуме и минимуме синусоиды делаются остановки-отпечатки, которые и есть логические состояния, НАРУШАЮЩИЕ линейность "синусоиды". Хранение отпечатка, состояния. и есть нарушение линейности движения перехода.
Составленные в "линию" последовательности состояний, нелинейны в принципе. "Линия", составленная из дискретов, состояний, может быть преобразована в "натуральное" линейное движение только если промежутки между состояниями будут ОДИНАКОВЫМИ.
Эти равные промежутки создаёт тактовый генератор.
Восстановленная из дискретов "прямая" всегда дискретна, и требует "интеграции".
Потому "нелинейная логика" - это уже, как минимум, "нелинейность нелинейности".
Думаю логика всегда, и только, линейна! Нелинейная логика это что то из разряда иррационального, недоступного моему пониманию.
Линейное устройство не "разводит" (не производит) нелинейность. Наличие нелинейности определяется множеством гармоник. Отсутствие нелинейности определяется только одной, действующей гармоникой, самой-собой, без появления "лишних" гармоник.
Дальше как хотите думайте))).
Если на синусоиде имеется две точки (максимум и минимум), то дальше всё линейнопрозрачно, будь там хоть десяток гармоник. Нелинейность живёт там, где эти две точки неопределены, вспомните себя на карусели, да хрен его знает, где юг, где север, до потери сознания... И выбраться из такой ситуации без нелинейности (это когда никакая логика не помогает, разве что тренировки) нет никакой возможности.
"Линейнопрозрачно" ДАЛЬШЕ будет только в высшей из "десятка гармоник", а не в низшей.
Ну да? Обычно уже с третьего аккорда всё понятно. :)
Природу (Котельникова) не объедешь. В реальности требуется не 2, а не менее трёх точек.)))
Что в записи {X | X не-равно Х} является элементом? Переменная Х при подстановке в нее значений. Можно ли говорить о не существовании Х без множества? Можно.
Таком образом,
пустое множество - это множество, в котором НЕ СУЩЕСТВУЕТ элементов Х тогда и только тогда, когда (Х не-равно Х)
заменяется на
НЕ СУЩЕСТВУЕТ Х тогда и только тогда, когда каждый Х выражен как (Х не-равно Х)