Главная › Записи › Записи bulygin69

Несепарабельные состояния

Аватар пользователя bulygin69
Систематизация и связи
Логика

Настоящая квантовая теория начинается там, где появляются несепарабельные состояния (неотделимости). 

Ссылка: http://quantmag.ppole.ru/QuantumMagic/Doronin/28.html

Комментарий:
Но что значит не-отделимости? 
То и значит, что два (или более) разных нечто начинают вести себя как одно (А & не-А = одно) 

И мало того, что А можно представить суперпозицией состояний |есть А> + |нет А>, 
а не-А можно представить также суперпозицией состояний |есть не-А> + |нет не-А>,
но еще возможно их смешение, смешение ранее независимых друг от друга систем А и не-А.
О диагональных элементах матрицы плотности можно сказать, что они примут значения 1/2

bulygin69, 21 Декабрь, 2016 - 07:26

Комментарии

Аватар пользователя Евгений Волков
Евгений Волков, 21 Декабрь, 2016 - 08:20, ссылка

Вы тоже состоите из множества элементов, но ведете себя как одно целое. это можно сказать про любую систему в мироздании, в том числе и в квантовой механике.

Аватар пользователя bulygin69
bulygin69, 21 Декабрь, 2016 - 08:34, ссылка

Матрица плотности

1) Сумма диагональных элементов, то есть след матрицы плотности равен единице
2) Эрмитовость - любая матрица плотности должна быть симметричной (в вещественном случае), ее недиагональные элементы расположены парами симметрично относительно главной диагонали. В комплексном случае эти пары будут комплексно сопряженными — это и есть эрмитова матрица
Такая симметричная структура матрицы плотности является следствием того,  что корреляции в системе всегда выступают парами: если одна подсистема взаимодействует с другой,  то и вторая коррелирует с первой — это одно и то же взаимодействие.  Только, когда речь идет о матрице плотности, более правильно говорить о наборе  различных основных состояний системы (диагональные элементы) и о корреляциях между ними (недиагональные элементы)
3) Положительная полуопределенность - Все собственные значения матрицы плотности вещественны (нет комплексных чисел) и неотрицательны (больше нуля или равны ему).  В случае чистых состояний ситуация еще проще — матрица плотности такого состояния  имеет только одно ненулевое собственное значение (равное единице), а все остальные равны нулю.

Аватар пользователя bulygin69
bulygin69, 21 Декабрь, 2016 - 08:46, ссылка

ссылка: http://dxdy.ru/topic58947.html

В такой матрице много элементов, глаза разбегаются, но суть её легко понять, если рассмотреть её как оператор (часто так прямо и обсуждают оператор плотности). Что будет, если умножить её слева на произвольный вектор-столбец? Вектор-строка $\langle\psi\rvert$ умножится на него, дав скалярное произведение, а последующий за ним вектор-столбец $\lvert\psi\rangle$ умножится на это скалярное произведение как на численный коэффициент. Итого, наш произвольный вектор-столбец будет рассмотрен в проекции на ось, и потом заменён на вектор вдоль этой оси, длиной в проекцию. То есть, наш оператор - это ровно проектор на направление, заданное исходным вектором состояния $\lvert\psi\rangle.$ Очевидно, он несёт столько же информации (у нас, может быть, потерялась комплексная фаза, но она в КМ и не нужна, поскольку не имеет физического смысла).

Саму КМ записать для нового способа представления просто: если у нас раньше был любой оператор эволюции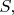 $S,$ действовавший $\lvert\psi\rangle\to S\lvert\psi\rangle,$ то теперь мы так же можем подействовать и на матрицу плотности: $\lvert\psi\rangle\langle\psi\rvert\to S\lvert\psi\rangle\langle\psi\rvert S^\dagger.$ Если раньше мы вычисляли среднее значение наблюдаемой как $\langle\psi\vert f\vert\psi\rangle,$ то сейчас должны взять $\operatorname{Tr}[f\lvert\psi\rangle\langle\psi\rvert].$ Разумеется, и от базиса к базису (в КМ терминологии - "от представления к представлению") мы тоже можем переходить без проблем. Вот и всех отличий.

Но на самом деле аппарат матрицы плотности шире по возможностям, чем аппарат векторов состояния. Если мы проделаем любые операции сложения с векторами состояния, мы снова получим вектор состояния - мы можем перейти от чистого состояния только к суперпозиции, которая в другом базисе снова будет чистым состоянием. Если же мы возьмём две матрицы плотности, то мы можем получить из них (просто линейной комбинацией) новую матрицу, которая по свойствам будет не хуже, чем исходные, но не будет отвечать никакому чистому состоянию, а будет называться смесью.