(Все А есть В) читается как ∀x(A(x) ⇒ B(x)), т.е (каждое Х, такое что: если Х-А, то Х-В) 
(Некоторые А есть В) читается как ∃x(A(x) & B(x)) т.е (хотя бы одно Х, такое что: Х-А и Х-В) 

Почему? Почему в прервом случае употребляется связка (если, то), а во втором (и)? Потому что импликация необходима, когда нужно выразить отношение (от конкретного к общему) на иерархии понятий. На связку (и) такого ограничения не налагается. 

Так, для примера из рисунка: 
1) Каждое Х, где Х ∈ {слон, собака, кошка}, такое что: если Х - зверь, то Х - животное. 
2) Хотя бы одно Х, где Х ∈ {слон, собака, кошка, муха, комар}, такое что: Х - зверь и Х - животное. 

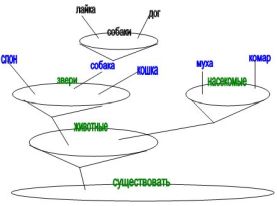
Разумеется, если Х ∈ {слон, собака, кошка}, то можно также сказать: ∃x(A(x) ⇒ B(x)) верно просто потому, что (каждый) является частным случаем для связки (хотя бы один). Т.е. имеем вырожденный случай: если нет лжи, если не расcматриваем (муху, комара), которые бы давали ложь (не существование): муха-зверь и муха-животное, комар-зверь и комар-животное.