Функция. Доказательство.

Решение.
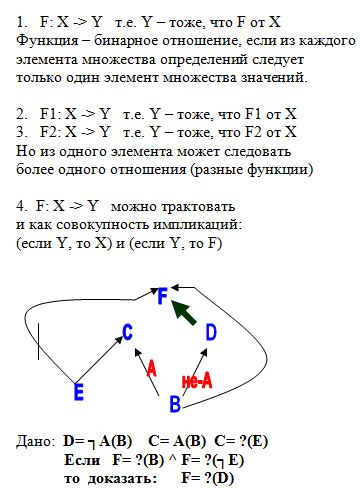
1. Прямое доказательство. F есть не-Е. F не есть E.
F не есть C. F не есть A(B). F есть не-А(В). F есть D.
2. Доказательство от противного. Пусть F есть не-D.
Тогда F есть не (не-А(В)). F есть А(В). F есть С.
F есть Е. Получили противоречие: F есть Е, F есть не-E.
Следовательно, (F есть не-D) ложно. Следовательно, F есть D
К таким же выводам можно прийти стандартным путем
- bulygin69
- Для комментирования войдите или зарегистрируйтесь

Комментарии
Само понимание сути Y=F(X) является той путеводной звездой, на
которую следует ориентироваться: «если к X применить F, то получим
только Y и ничто иное». Если же это не так, т.е. получили «если к X
применили F и получили как Y, так и нечто иное», то тогда неверно, что
F(X)->Y.
Для примера рассмотрим доказательство теоремы Пифагора.
Имеется треугольник АВС с прямым углом В. Проведем высоту из угла В
и обозначим ее основание через D. Имеем cos(А)=AD/AB=AB/AC и
cos(C)=DC/BC=BC/AC.
Применим функцию F такую, что умножим (свойство пропорции)
числитель одной дроби на знаменатель другой дроби. Получим (только),
что квадрат стороны АВ равен произведению сторон AD и AC. И получим
(только), что квадрат стороны ВС равен произведению сторон DC и AC.
Далее применим к этим равенствам другую функцию F такую, что сложим
эти равенства почленно. В результате получим (только), что квадрат
стороны АС(гипотенуза) равен сумме квадратов сторон АВ и ВС
(катетов).
Хотя в самом общем виде не вызывает затруднений как можно и
нужно строить доказательство, выбор конкретной функции F остается
весьма трудным делом
Конструирование натурального ряда (нодь -> первый->второй->и т.д.) с учетом Y=F(X) или, что то же, F(X)->Y таково:
F – внесение различия по отношению к предыдущим элементам натурального ряда, а X - изначально то, что «не равно себе». И на каждом последующем шаге вместо X подставляется полученное на предыдущем шаге Y.
Когда говорят, что между объектами ничего нет, означает, что
между объектами есть это ничего. И это ничего есть ничто иное как
граница. С точки зрения описания существующих объектов
(преобразований) границу объекта следует внести в описание объекта.
На самом деле так и поступают, например, рассматривая объекты на языке
UML, когда состояние нет_Х преобразования Х обозначают состояниями
entry и exit. Причем, эти особенные состояния иногда рисуются на
диаграммах состояний как внутри объекта, так и вовне объекта. Что еще
раз подчеркивает суть нуля (нуля объекта Х) как границы Х и не-Х. И что
логически выражается как: «Х равно не-Х» или «Х не-равно Х».
В доказательствах от противного это всегда ложное «Х не-равно Х» используется, если нужно выразить то, чего нет.
С этого же (всегда ложного) начинается конструирование чисел натурального ряда.