АННОТАЦИЯ
В работе предпринята попытка абстрактного математического построения вариационного принципа, пригодного для получения уравнений полей, аналогичных гравитационному и электромагнитному. Особенностью метода исследования является абстрагирование от любых эмпирических обобщений. Все результаты получены в виде математических следствий гипотезы неодновременности, принципа необратимости времени и принципа наиболее вероятной цепи событий.
ABSTRACT
There is an attempt of abstract mathematical construction of the variational principle, adequate for the reception fields equations similar gravitational and electromagnetic is undertaken in the given work. Feature of the analysis is abstraction from any empirical generalizations. All results are received as mathematical consequences of non-simultaneity hypothesis, the principle of irreversibility of time and the principle of the most probable succession of events.
Как может конкретная реальность превратиться в абстрактную, да ещё и математическую? Возможно это оборотная сторона вопроса о том, как абстрактные математические понятия могут становиться почти ощутимо реальными в мире Платона. Возможно, в каком-то смысле, эти два мира, на самом деле - один и тот же мир?
Р.Пенроуз "Новый ум короля"
ВВЕДЕНИЕ
Данная работа является продолжением [1]. Исследуются динамические законы взаимодействия подсистем системы времени [2]. Метод исследования состоит в дедуктивном выводе и анализе абстрактных математических следствий гипотезы неодновременности и принципа необратимости времени.
Рассматривается система с наблюдателем, моделируемая автоматом, взаимодействующим со случайной средой в дискретном времени. Все состояния среды и автомата, согласно гипотезе неодновременности, считаются линейно упорядочеными в цепи событий. Исследуемую модель можно представить в виде автомата, на вход которого с бесконечной, проходящей через него, ленты поступает линейно упорядоченная последовательность символов (состояний среды). Состояния автомата, являющиеся следствиями предшествующих состояний среды и его самого, отображаются на этой же ленте, моделирующей по отношению к автомату – наблюдателю “течение” времени. В качестве исходных принимаются определения, допущения и результаты работы [1]. В том числе предполагается псевдоконтинуальность цепи событий.
В качестве подсистем рассматриваются подмножества цепи событий. Взаимодействие между подсистемами состоит в обмене состояниями. Вследствие линейной упорядоченности цепи событий, в каждый момент времени происходит переход из одного состояния в другое, в том числе из состояния одной подсистемы в состояние другой. В этом проявляется причинно-следственная связь (взаимодействие) подсистем системы времени. Подсистемы как бы обмениваются состояниями – переносчиками взаимодействия. Так как скорости изменения состояний измеряются относительными количествами (частотами) их повторений в цепи событий, то измеряя изменения этих количеств и их отношение к количеству событий (времени) системы начала отсчёта, можно получить распределение величин ускорений в собственном пространстве системы времени. Это распределение является математическим эквивалентом силового поля. Так как неизменность количеств повторяющихся состояний на различных участках произвольной цепи событий - скорее исключение чем правило, то можно считать, что в общем случае силовое поле всегда присутствует в собственном пространстве системы времени. С другой стороны, бессмысленно ставить вопрос о каких-то математических закономерностях подобного поля в совершенно произвольной системе. Наблюдатель произвольной системы может обнаружить определённые закономерности её движений, лишь ограничив область своих наблюдений некоторым классом подсистем. Такой подход, когда рассматриваются не все возможные подсистемы данной системы, а лишь те, которые удовлетворяют некоторому, объединяющему их условию, известен в динамике как принцип наименьшего действия. Согласно этому принципу рассматривается такое подмножество подсистем данной системы, чьё взаимосвязанное движение минимизирует функционал вполне определённого вида. Теории электромагнитного и гравитационного полей выделяют два различных класса подсистем, чьё взаимное движение минимизирует соответствующие функционалы двух разных видов. Но уже сейчас физике известны и другие поля, а, следовательно, и другие классы подсистем и другие функционалы. Не исключено, что удастся найти функционал, объединяющий все известные динамические группы в одну, но при этом всё равно не исключается возможность существования иных (ещё не обнаруженных) динамических групп, не удовлетворяющих найденному функционалу. В математических (кибернетических) теориях динамических систем [3] функционал символизирует цель движения. Можно ли допустить, что произвольная система подчинена какой-то одной цели относительного движения её подсистем? Такого рода предположение выглядит сомнительно. В нём присутствует внутреннее противоречие. Если система произвольна, то о какой общей цели можно говорить? Если же имеется единая цель, то система уже не произвольная. Таким образом, мы приходим к выводу о принципиальной невозможности детерминированного описания произвольной системы в целом с помощью одного функционала.
Но можно подойти к решению поставленной задачи иначе.
ПРИНЦИП НАИБОЛЕЕ ВЕРОЯТНОЙ ЦЕПИ СОБЫТИЙ
В [1] было показано, что относительные скорости движения подсистем системы времени определяются распределением относительных количеств (частот) повторяющихся состояний в цепи событий. При этом параметры движения (скорости и их производные) инвариантны к порядку следования состояний. Рассматривая отрезок цепи событий, мы, по определению [2], измеряем изменения координат подсистем на этом участке изменением количеств соответствующих состояний, не учитывая последовательность их появления в цепи событий. Но это означает, что одному и тому же промежутку времени могут соответствовать разные последовательности состояний одной и той же в динамическом отношении системы. Не составляет труда определить количество 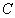 таких последовательностей состояний для заданного распределения частот состояний на отрезке цепи событий.
таких последовательностей состояний для заданного распределения частот состояний на отрезке цепи событий.
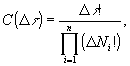 (1)
(1)
где 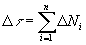 - количество событий (моментов времени),
- количество событий (моментов времени), 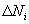 - количество повторений
- количество повторений 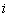 - того состояния на рассматриваемом отрезке цепи событий.
- того состояния на рассматриваемом отрезке цепи событий.
Здесь пока что система рассматривается с точки зрения внешнего наблюдателя, для которого время измеряется количеством всех событий в системе (для внутреннего наблюдателя время измеряется количеством событий в подсистеме, которая выбрана в качестве объекта начала отсчёта [1]).
Если последовательность состояний в цепи событий интерпретировать как некое сообщение, то логарифм величины 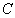 с точностью до масштабного множителя
с точностью до масштабного множителя 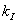 определяет количество информации
определяет количество информации 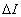 в этом сообщении.
в этом сообщении.
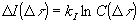 . (2)
. (2)
Отношение количества последовательностей состояний, допустимых при заданном распределении их частот повторений, к количеству всех возможных последовательностей состояний определяет вероятность цепи событий системы времени. Чем больше имеется способов реализации одного и того же относительного движения подсистемы различными последовательностями состояний, тем с большей вероятностью именно это движение будет воспринято наблюдателем. Следовательно, можно поставить задачу найти такое динамическое взаимодействие подсистем в системе времени, которое максимизирует вероятность цепи событий. Однако, цепь событий произвольной системы времени в общем случае не является ни наиболее ни наименее вероятной. Тем не менее, всегда можно представить произвольную цепь событий объединением двух цепей, одна из которых является наиболее вероятной. Так как распределение скоростей и ускорений в собственном пространстве системы определяется распределением частот состояний в цепи событий, то внутренний наблюдатель будет чаще наблюдать те траектории движения и то силовое поле, которые соответствуют наиболее вероятной цепи событий. Та же часть системы, чьи состояния образуют менее вероятную цепь событий, отвечает заотносительно редкие случайные отклонения динамической картины мира внутреннего наблюдателя от той, которая определена наиболее вероятной цепью событий. Таким образом, принцип наиболее вероятной цеписобытий, с одной стороны, выделяет некоторым детерминированным образом динамическую группу движений с определённой симметрией, а с другой стороны, не исключает случайности, проявляющейся в нарушениях этой симметрии.
Для того, чтобы придать принципу наиболее вероятной цепи событий математическое содержание, необходимо указать максимизируемый функционал и ограничения, которым должна удовлетворять цепь событий.
ФУНКЦИОНАЛ НАИБОЛЕЕ ВЕРОЯТНОЙ ЦЕПИ СОБЫТИЙ
Согласно (1) наиболее вероятной цепи событий соответствует наибольшее значение 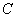 . Однако, непосредственное использование этой величины в качестве максимизируемого интегрального критерия затруднено из за её неаддитивности. Пусть, например, цепь событий разбита на подцепи так что
. Однако, непосредственное использование этой величины в качестве максимизируемого интегрального критерия затруднено из за её неаддитивности. Пусть, например, цепь событий разбита на подцепи так что 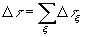 , где
, где 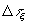 - количество событий в
- количество событий в 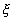 - той подцепи. В таком случае
- той подцепи. В таком случае
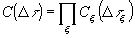 . (3)
. (3)
Напротив, количество информации 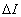 удовлетворяет требованию аддитивности
удовлетворяет требованию аддитивности
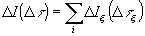 . (4)
. (4)
Вследствие монотонности логарифмической функции максимальные значения (3) и (4) взаимно однозначно соответствуют друг другу. Это значит, что если некое распределение состояний в цепи событий доставляет максимум (4), то при этом же распределении достигается максимум и в (3).
В предельном случае (псевдоконтинуальность) сумму можно заменить интегралом
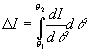 , (5)
, (5)
где 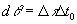 - приращение собственного времени всей системы в целом [1].
- приращение собственного времени всей системы в целом [1].
Для того, чтобы найти значение производной под знаком интеграла, разделим правую и левую части равенства (2) на 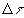 . Логарифмируя, получим
. Логарифмируя, получим
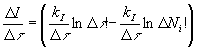 . (6)
. (6)
Так как в связи с условием псевдоконтинуальности все 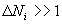 ,
, 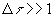 , а вследствие линейной упорядоченности состояний (гипотеза неодновременности)
, а вследствие линейной упорядоченности состояний (гипотеза неодновременности) 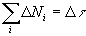 , то, применяя формулу Стирлинга, можно записать
, то, применяя формулу Стирлинга, можно записать
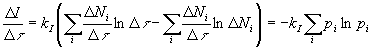 , (7)
, (7)
где 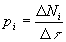 - вероятность появления
- вероятность появления 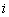 - того состояния на отрезке цепи событий.
- того состояния на отрезке цепи событий.
Правая часть (7) представляет собой Шенноновскую [4] энтропию 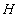 сообщения, получаемого наблюдателем с пресловутой “ленты времени”. Умножив и разделив левую часть (7) на квант времени
сообщения, получаемого наблюдателем с пресловутой “ленты времени”. Умножив и разделив левую часть (7) на квант времени 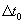 , получим в пределе
, получим в пределе
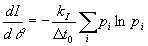 , (8)
, (8)
где 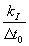 - постоянная, имеющая размерность бит/сек .
- постоянная, имеющая размерность бит/сек .
Таким образом, условие наиболее вероятной цепи событий записывается в виде
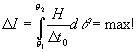 (9)
(9)
Это же условие, при замене знака перед интегралом на противоположный, может быть записано в виде, аналогичном принципу наименьшего действия
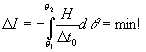 (10)
(10)
Однако здесь действие измеряется количеством информации, т.е., согласно классическому определению [4], логарифмом количества возможных сообщений (цепей событий) при заданном алфавите и распределении символов (состояний). Если данному набору состояний соответствует лишь одна возможная цепь событий, то количество информации в ней равно нулю. Но дробных количеств цепей событий (равно как и сообщений) быть не может по определению. Наименьшим количеством информации обладает набор состояний, допускающий лишь две возможные цепи событий. Следовательно, количество информации – квантованная величина, обычно измеряемая в битах. Учитывая, что квант информации равен одному биту, а квант физического действия – величине постоянной Планка 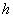 , можно перейти к физической размерности действия, умножив информационную энтропию на константу
, можно перейти к физической размерности действия, умножив информационную энтропию на константу 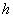 .
.
До сих пор мы предполагали, что система рассматривается с точки зрения внешнего наблюдателя, измеряя время количеством всех событий в системе. Так как нас интересует внутренняя динамика системы, рассматриваемая относительно внутреннего наблюдателя, необходимо в (10) перейти к его собственному времени 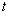 , измеряемому количеством событий в некоторой
, измеряемому количеством событий в некоторой 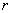 - той подсистеме, выбранной в качестве объекта начала отсчёта. При этом
- той подсистеме, выбранной в качестве объекта начала отсчёта. При этом
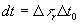 . Произведя замену переменной в (10), получим действие
. Произведя замену переменной в (10), получим действие 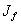 относительно внутреннего наблюдателя в физических единицах
относительно внутреннего наблюдателя в физических единицах
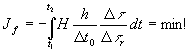 (11)
(11)
Величина
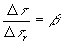 (12)
(12)
представляет собой отношение собственного времени системы к собственному времени внутреннего наблюдателя. Заметим также, что переход к другому внутреннему наблюдателю приводит к изменению отношения 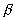 и оставляет неизменным действие (11). Вследствие линейной упорядоченности событий (гипотеза неодновременности) имеем:
и оставляет неизменным действие (11). Вследствие линейной упорядоченности событий (гипотеза неодновременности) имеем: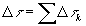 . Поэтому функционал (11) можно представить в виде суммы
. Поэтому функционал (11) можно представить в виде суммы
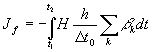 , (13)
, (13)
где индексом 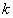 обозначена одна из наблюдаемых подсистем.
обозначена одна из наблюдаемых подсистем.
Согласно результатам полученным в [1], интервал 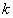 - той подсистемы в пространстве событий общего вида (искривлённом) может быть представлен следующими равенствами
- той подсистемы в пространстве событий общего вида (искривлённом) может быть представлен следующими равенствами
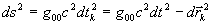 , (14)
, (14)
где 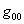 - компонент метрического тензора в рассматриваемой точке пространства событий,
- компонент метрического тензора в рассматриваемой точке пространства событий, 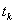 - собственное время
- собственное время 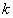 - той подсистемы,
- той подсистемы, 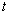 - собственное время наблюдателя,
- собственное время наблюдателя, 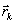 - радиус-вектор
- радиус-вектор 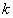 - той подсистемы.
- той подсистемы.
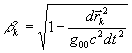 . (15)
. (15)
С учётом кривизны пространства событий имеем
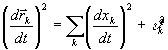 , (16)
, (16)
где 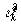 - некоторая функция координат и времени. С учётом последнего равенства отношение собственных времён наблюдаемой подсистемы и наблюдателя может быть записано в виде
- некоторая функция координат и времени. С учётом последнего равенства отношение собственных времён наблюдаемой подсистемы и наблюдателя может быть записано в виде
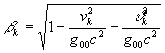 , (17)
, (17)
где 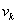 - скорость
- скорость 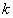 -той подсистемы относительно внутреннего наблюдателя. Умножив и разделив правую часть на постоянную
-той подсистемы относительно внутреннего наблюдателя. Умножив и разделив правую часть на постоянную 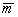 и раскладывая её в степенной ряд с точностью до членов второго порядка, получим
и раскладывая её в степенной ряд с точностью до членов второго порядка, получим
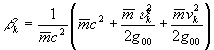 . (18)
. (18)
Здесь величина 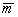 формально имеет значение средней массы подсистемы (определение понятия массы подсистемы как параметра, характеризующего распределение состояний в цепи событий будет дано ниже). Суммируя по всем индексам
формально имеет значение средней массы подсистемы (определение понятия массы подсистемы как параметра, характеризующего распределение состояний в цепи событий будет дано ниже). Суммируя по всем индексам 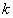 , и выразив сумму через средние значения, получим
, и выразив сумму через средние значения, получим
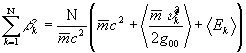 , (19)
, (19)
где 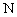 - количество подсистем.
- количество подсистем.
В этом выражении величина 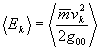 соответствует той части средней (кинетической) энергии подсистем в составе наблюдаемой системы, которая обусловлена их относительным движением. Величина
соответствует той части средней (кинетической) энергии подсистем в составе наблюдаемой системы, которая обусловлена их относительным движением. Величина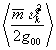 соответствует той части средней энергии подсистем, которая обусловлена кривизной пространства событий. Действительно, в плоском пространстве всюду
соответствует той части средней энергии подсистем, которая обусловлена кривизной пространства событий. Действительно, в плоском пространстве всюду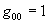 и
и 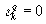 . При этом
. При этом
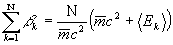 . (20)
. (20)
По аналогии с молекулярно кинетической теорией величину средней кинетической энергии будем с точностью до масштабного множителя измерять величиной температуры системы
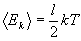 , (21)
, (21)
где 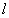 - число степеней свободы подсистемы (количество различных (неповторяющихся) состояний, в которых может оказываться подсистема в цепи событий).
- число степеней свободы подсистемы (количество различных (неповторяющихся) состояний, в которых может оказываться подсистема в цепи событий).
Принимая константу 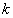 , равной постоянной Больцмана, получим величину температуры в градусах.
, равной постоянной Больцмана, получим величину температуры в градусах.
Рассматривая систему в целом, мы полагаем её замкнутой. В однородном времени функция Лагранжа замкнутой системы 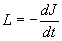 не зависит от времени явно. Отсюда следует существование интеграла движения, называемого энергией системы
не зависит от времени явно. Отсюда следует существование интеграла движения, называемого энергией системы
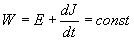 , (22)
, (22)
где 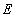 - квадратичная функция скоростей.
- квадратичная функция скоростей.
Выше было дано определение действию как произведению количества информации на постоянную Планка. При этом одному биту информации соответствует один квант действия. Следовательно, функцию Лагранжа можно представить в виде
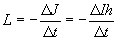 . (23)
. (23)
Рассматривая систему в целом, мы полагаем её неподвижной относительно наблюдателя. Энергия покоящейся системы равна 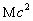 , где
, где 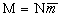 . Эта энергия не зависит от того, какое количество информации производится в системе. Следовательно, интеграл движения при производстве одного бита информации (данному набору состояний соответствует лишь две возможные цепи событий) имеет вид
. Эта энергия не зависит от того, какое количество информации производится в системе. Следовательно, интеграл движения при производстве одного бита информации (данному набору состояний соответствует лишь две возможные цепи событий) имеет вид
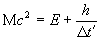 . (24)
. (24)
Так как 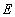 - положительно определённая квадратичная функция, то наибольшее значение отношения
- положительно определённая квадратичная функция, то наибольшее значение отношения 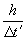 будет достигаться при
будет достигаться при 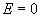 . Но наибольшему значению этого отношения соответствует наименьшее возможное приращение времени – квант
. Но наибольшему значению этого отношения соответствует наименьшее возможное приращение времени – квант 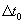 . Следовательно,
. Следовательно,
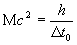 . (25)
. (25)
Подставляя (19) в (13) и учтя (25), найдём
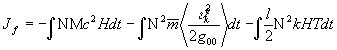 . (26)
. (26)
Обозначая физическую энтропию
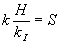 , (27)
, (27)
и подставляя её в (26), получим
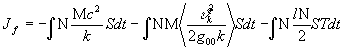 , (28)
, (28)
где 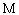 - масса системы в целом, а множитель
- масса системы в целом, а множитель 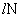 представляет собой количество её степеней свободы.
представляет собой количество её степеней свободы.
Обе эти величины не зависят от способа декомпозиции системы на подсистемы. Множитель 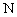 является неопределённым, так как любую систему можно представлять состоящей из различного количества подсистем, по-разному комбинируя их составные части. Если рассматриваются такие виды взаимодействий, при которых количество подсистем не изменяется, то этим множителем при выводе уравнений поля можно пренебречь. Если же рассматриваются взаимодействия, связанные с процессами синтеза или распада подсистем, то он должен быть учтён при выводе уравнений поля. В связи с этим можно ввести понятие структурного равновесия системы, условием которого является
является неопределённым, так как любую систему можно представлять состоящей из различного количества подсистем, по-разному комбинируя их составные части. Если рассматриваются такие виды взаимодействий, при которых количество подсистем не изменяется, то этим множителем при выводе уравнений поля можно пренебречь. Если же рассматриваются взаимодействия, связанные с процессами синтеза или распада подсистем, то он должен быть учтён при выводе уравнений поля. В связи с этим можно ввести понятие структурного равновесия системы, условием которого является 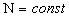 . В структурно неравновесных системах процессы синтеза и распада подсистем взаимно не уравновешиваются и это условие не выполняется. Следовательно, уравнения поля структурно равновесных и неравновесных систем должны отличаться друг от друга. Может быть именно влиянием на электромагнитное и гравитационное поля неуравновешенных процессов синтеза и распада подсистем материального мира можно объяснить аномалии, зафиксированные в экспериментах Н.А.Козырева и С.Э.Шноля?
. В структурно неравновесных системах процессы синтеза и распада подсистем взаимно не уравновешиваются и это условие не выполняется. Следовательно, уравнения поля структурно равновесных и неравновесных систем должны отличаться друг от друга. Может быть именно влиянием на электромагнитное и гравитационное поля неуравновешенных процессов синтеза и распада подсистем материального мира можно объяснить аномалии, зафиксированные в экспериментах Н.А.Козырева и С.Э.Шноля?
Итак, мы получили функционал действия системы, определяющий её наиболее вероятную цепь событий, в виде суммы трёх слагаемых. Сгруппируем их по признаку отношения к кривизне пространства событий
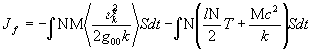 . (29)
. (29)
В этом функционале первое слагаемое присутствует лишь тогда, когда учитывается кривизна пространства событий. В плоском пространстве оно тождественно обращается в нуль. Второе слагаемое остаётся частью действия как в плоском так и в искривлённом пространстве. Нормируя температуру 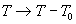 таким образом, чтобы её нуль соответствовал энергии покоя системы
таким образом, чтобы её нуль соответствовал энергии покоя системы 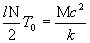 , получим
, получим
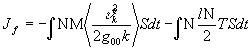 . (30)
. (30)
По аналогии с кинетической температурой 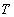 можно ввести понятие гравитационной температуры
можно ввести понятие гравитационной температуры 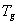 такой, что
такой, что 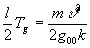 . При этом функционал приводится к виду
. При этом функционал приводится к виду
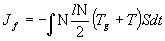 . (31)
. (31)
Гравитационная температура служит мерой дополнительной средней энергии относительного движения подсистем, обусловленной кривизной пространства событий. В плоском пространстве она равна нулю.
УРАВНЕНИЯ ДВИЖЕНИЯ ПОДСИСТЕМ
Уравнения движения и уравнения общего поля могут быть получены варьированием функционала наиболее вероятной цепи событий. Однако, при этом должны быть учтены ограничения, накладываемые закономерностями цепи событий на возможные траектории движения подсистем системы времени. Учёт ограничений принципиально отличает принцип наиболее вероятной цепи событий от принципа наименьшего действия. В [1] была выведена в качестве основного следствия гипотезы неодновременности закономерность, согласно которой собственное время подсистемы пропорционально количеству всех её состояний на отрезке цепи событий, заключённом между двумя фиксированными событиями, по которым производится отсчёт времени
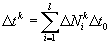 , (32)
, (32)
где 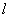 - размерность подсистемы.
- размерность подсистемы.
Выразим величины 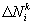 через приращения координат и времени, измеряемые внутренним наблюдателем (согласно основному уравнению состояния внутреннего наблюдателя [1])
через приращения координат и времени, измеряемые внутренним наблюдателем (согласно основному уравнению состояния внутреннего наблюдателя [1])
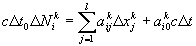 , (33)
, (33)
где 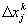 - приращения координат
- приращения координат 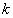 - той подсистемы, измеряемые внутренним наблюдателем,
- той подсистемы, измеряемые внутренним наблюдателем, 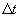 - приращение собственного времени внутреннего наблюдателя,
- приращение собственного времени внутреннего наблюдателя, 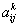 - коэффициенты взаимного преобразования систем отсчёта внутреннего и внешнего наблюдателей. Здесь индекс
- коэффициенты взаимного преобразования систем отсчёта внутреннего и внешнего наблюдателей. Здесь индекс 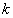 указывает на то, что преобразование осуществляется в той точке пространства событий
указывает на то, что преобразование осуществляется в той точке пространства событий 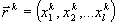 , где находится
, где находится 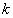 - тая подсистема.
- тая подсистема.
Суммируя правые и левые части уравнений (33) и переходя к пределу, получим для произвольной точки пространства событий, в которой может оказаться подсистема
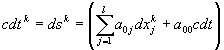 , (34)
, (34)
где:
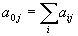 , (35)
, (35)
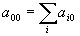 , (36)
, (36)
Интегрируя (34), получим
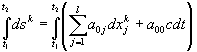 . (37)
. (37)
Этим уравнением накладывается первое ограничение на допустимую траекторию 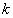 - той подсистемы. Второе ограничение связано с необратимостью времени
- той подсистемы. Второе ограничение связано с необратимостью времени 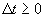 и имеет вид неравенства
и имеет вид неравенства
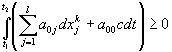 . (38)
. (38)
Заметим, что несмотря на кажущуюся тавтологию, второе ограничение не зависит от первого, так как 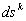 может иметь любой знак, независимо от траектории
может иметь любой знак, независимо от траектории 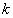 - той подсистемы. Экстремали функционала
- той подсистемы. Экстремали функционала 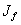 , полученные без учёта ограничений (37) и (38) не соответствуют истинным траекториям подсистем. Для того, чтобы найти истинные траектории, необходимо решить, так называемую, условно экстремальную задачу с ограничениями
, полученные без учёта ограничений (37) и (38) не соответствуют истинным траекториям подсистем. Для того, чтобы найти истинные траектории, необходимо решить, так называемую, условно экстремальную задачу с ограничениями 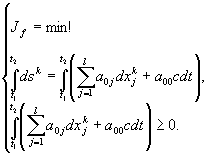 (39)
(39)
Как известно, решения подобной задачи должны минимизировать функционал вида
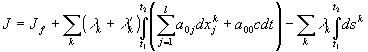 , (40)
, (40)
где 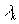 ,
, 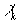 - множители Лагранжа. Причём,
- множители Лагранжа. Причём, 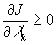 .
.
Области допустимых значений множителей Лагранжа могут быть определены, исходя из возможности достижения минимума функционала (40). Выберем такую систему отсчёта, в которой 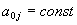 ,
, 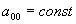 . При этом
. При этом
траектория подсистемы определяется из условия 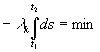 , что соответствует её свободному движению. Интеграл
, что соответствует её свободному движению. Интеграл 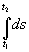 , как известно, имеет максимальное значение вдоль прямой мировой линии. Интегрируя вдоль кривой мировой линии можно сделать его сколь угодно малым. Следовательно, интеграл, взятый с положительным знаком не может иметь минимума. Таким образом, множитель Лагранжа
, как известно, имеет максимальное значение вдоль прямой мировой линии. Интегрируя вдоль кривой мировой линии можно сделать его сколь угодно малым. Следовательно, интеграл, взятый с положительным знаком не может иметь минимума. Таким образом, множитель Лагранжа 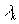 может принимать только положительные значения. Так как множители Лагранжа по определению являются инвариантами, то положительная определённость
может принимать только положительные значения. Так как множители Лагранжа по определению являются инвариантами, то положительная определённость 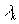 сохраняется и в любой иной системе отсчёта. В отношении
сохраняется и в любой иной системе отсчёта. В отношении 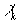 подобные ограничения отсутствуют. Следовательно, этот множитель Лагранжа может принимать как положительные, так и отрицательные значения.
подобные ограничения отсутствуют. Следовательно, этот множитель Лагранжа может принимать как положительные, так и отрицательные значения.
Обозначим:
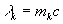 , (41)
, (41)
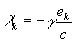 . (42)
. (42)
где, 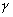 - масштабный коэффициент, учитывающий единицы измерения.
- масштабный коэффициент, учитывающий единицы измерения.
Постоянная 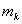 аналогична по смыслу массе частицы, Сумма множителей Лагранжа
аналогична по смыслу массе частицы, Сумма множителей Лагранжа
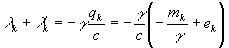 (43)
(43)
с точностью до множителя 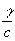 аналогична заряду частицы
аналогична заряду частицы 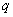 .
.
Подставляя (43) в (40), получим
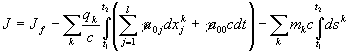 . (44)
. (44)
Множители Лагранжа в условно экстремальной задаче с ограничениями типа неравенств определяют внутреннюю область допустимых траекторий подсистемы. Для того, чтобы их найти, необходимо исследовать граничные условия, задаваемые (37) и (38). При такой постановке задачи зависимость потенциалов поля 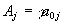 (
(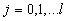 ) и их производных от координат и времени предполагается известной. Однако в физике обычно рассматривается иная задача, состоящая в том, чтобы найти траектории подсистем и уравнения поля (зависимость потенциалов поля и их производных от координат и времени), при заданном начальном распределении масс и зарядов в пространстве – времени. Задавая заряды и массы всех подсистем (множители Лагранжа), мы косвенным образом ограничиваем область, которая соответствует наиболее вероятной цепи событий. Таким образом, величины масс и зарядов непосредственно связаны с граничными условиями, определяющими пространственно – временную область существования системы времени.
) и их производных от координат и времени предполагается известной. Однако в физике обычно рассматривается иная задача, состоящая в том, чтобы найти траектории подсистем и уравнения поля (зависимость потенциалов поля и их производных от координат и времени), при заданном начальном распределении масс и зарядов в пространстве – времени. Задавая заряды и массы всех подсистем (множители Лагранжа), мы косвенным образом ограничиваем область, которая соответствует наиболее вероятной цепи событий. Таким образом, величины масс и зарядов непосредственно связаны с граничными условиями, определяющими пространственно – временную область существования системы времени.
Варьируя траектории в искривлённом (в общем случае) пространстве, получим тензорные уравнения движения подсистем в виде, аналогичном известным уравнениям электродинамики
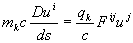 , (45)
, (45)
где: 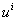 - компонента вектора скорости подсистемы;
- компонента вектора скорости подсистемы; 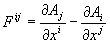 - тензор
- тензор
общего поля; 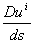 - ковариантная производная
- ковариантная производная
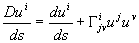 ; (46)
; (46)
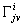 - символы Кристоффеля;
- символы Кристоффеля; 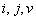 - индексы, принимающие независимо друг от друга значения от 0 до
- индексы, принимающие независимо друг от друга значения от 0 до 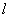 .
.
Из (45) видно, что уравнения относительного движения подсистемы системы времени аналогичны уравнениям электродинамики для частицы массой 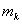 , несущей заряд
, несущей заряд 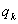 в гравитационном и электромагнитном полях. Однако, в отличие от классической электродинамики здесь в качестве эквивалента электрического заряда выступает сумма
в гравитационном и электромагнитном полях. Однако, в отличие от классической электродинамики здесь в качестве эквивалента электрического заряда выступает сумма 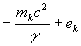 . Следовательно, электромагнитное взаимодействие подсистем системы времени можно представить в виде суммы двух взаимодействий. Одно из них порождается виртуальными зарядами электричества
. Следовательно, электромагнитное взаимодействие подсистем системы времени можно представить в виде суммы двух взаимодействий. Одно из них порождается виртуальными зарядами электричества 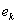 , а второе – виртуальными зарядами масс
, а второе – виртуальными зарядами масс 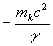 . Общее поле системы, как видно из (45) и (47), включает также гравитационную составляющую, обусловленную кривизной пространства событий. Таким образом, с точки зрения гипотезы неодновременности, масса играет двоякую роль. С одной стороны, она участвует в межчастичных взаимодействиях, являясь одной из составляющих электрического заряда, а с другой – выступает в качестве источника гравитационного взаимодействия, искривляя пространство событий. Следует также отметить ещё одну немаловажную деталь. Потенциалы электромагнитного поля системы времени являются линейными функциями элементов матрицы
. Общее поле системы, как видно из (45) и (47), включает также гравитационную составляющую, обусловленную кривизной пространства событий. Таким образом, с точки зрения гипотезы неодновременности, масса играет двоякую роль. С одной стороны, она участвует в межчастичных взаимодействиях, являясь одной из составляющих электрического заряда, а с другой – выступает в качестве источника гравитационного взаимодействия, искривляя пространство событий. Следует также отметить ещё одну немаловажную деталь. Потенциалы электромагнитного поля системы времени являются линейными функциями элементов матрицы 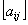 . Следовательно, в плоском пространстве, где
. Следовательно, в плоском пространстве, где 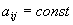 , тензор электромагнитного поля равен нулю, т.е. поле отсутствует. Поэтому известные уравнения поля, выведенные для плоского пространства, с точки зрения гипотезы неодновременности следует рассматривать как Максквеллов предел
, тензор электромагнитного поля равен нулю, т.е. поле отсутствует. Поэтому известные уравнения поля, выведенные для плоского пространства, с точки зрения гипотезы неодновременности следует рассматривать как Максквеллов предел 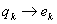 ,
,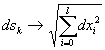 , соответствующий случаю, когда виртуальным зарядом массы и кривизной пространства событий можно пренебречь
, соответствующий случаю, когда виртуальным зарядом массы и кривизной пространства событий можно пренебречь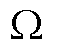 ,
, 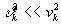 . Отличия электродинамики системы времени от классической, обусловленные наличием виртуального заряда массы представляют отдельную тему для исследований, выходящих за рамки данной работы.
. Отличия электродинамики системы времени от классической, обусловленные наличием виртуального заряда массы представляют отдельную тему для исследований, выходящих за рамки данной работы.
Прежде чем перейти к выводу уравнений общего поля, отметим ту роль, которую играет необратимость времени в явлении электромагнетизма.
Действительно, в отсутствии ограничения (38), являющегося математическим выражением необратимости, электромагнитный заряд подсистемы 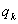 становится эквивалентом массы (исчезает множитель Лагранжа
становится эквивалентом массы (исчезает множитель Лагранжа 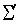 для всех подсистем). В этом случае уравнения движения описывают движение частиц в одном лишь гравитационном поле, а электромагнитное взаимодействие вырождается. Причём, как видно из уравнений (45), при
для всех подсистем). В этом случае уравнения движения описывают движение частиц в одном лишь гравитационном поле, а электромагнитное взаимодействие вырождается. Причём, как видно из уравнений (45), при 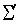 =0 траектории подсистем обезличены, их можно различать лишь по разным начальным условиям, ускорения в каждой точке пространства определяются только гравитационным полем (принцип эквивалентности гравитационной и инертной массы).
=0 траектории подсистем обезличены, их можно различать лишь по разным начальным условиям, ускорения в каждой точке пространства определяются только гравитационным полем (принцип эквивалентности гравитационной и инертной массы).
УРАВНЕНИЯ ОБЩЕГО ПОЛЯ
Та часть функционала наиболее вероятной цепи событий, которая характеризует действие общего поля 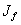 , не зависит явно от траекторий отдельных подсистем и поэтому не влияет на уравнения их движения (45). Однако, она становится необходимой, когда мы хотим найти уравнения самого поля. Для того, чтобы решить эту задачу, необходимо выразить действие поля через его потенциалы.
, не зависит явно от траекторий отдельных подсистем и поэтому не влияет на уравнения их движения (45). Однако, она становится необходимой, когда мы хотим найти уравнения самого поля. Для того, чтобы решить эту задачу, необходимо выразить действие поля через его потенциалы.
Как было показано выше, действие общего поля представляет собой сумму
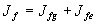 , (47)
, (47)
где: 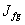 - та часть действия, которая обусловлена кривизной пространства событий,
- та часть действия, которая обусловлена кривизной пространства событий, 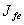 - та часть действия, которая не исчезает в плоском пространстве событий.
- та часть действия, которая не исчезает в плоском пространстве событий.
Как видно из (44), переменными общего поля являются величины 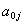 (
(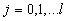 ), входящие во второе слагаемое и компоненты метрического тензора
), входящие во второе слагаемое и компоненты метрического тензора 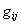 , входящие в третье слагаемое. Сами эти переменные, в свою очередь, могут быть выражены через компоненты матрицы
, входящие в третье слагаемое. Сами эти переменные, в свою очередь, могут быть выражены через компоненты матрицы 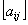 , отображающей пространство событий внутреннего наблюдателя в пространство событий внешнего.
, отображающей пространство событий внутреннего наблюдателя в пространство событий внешнего.
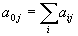 , (48)
, (48)
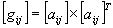 . (49)
. (49)
В связи с этим матрицу 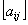 будем называть матрицей общего поля системы времени, а порождаемые ею величины
будем называть матрицей общего поля системы времени, а порождаемые ею величины 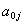 и
и 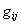 – соответственно потенциалами общего электромагнитного и гравитационного полей. Заметим, что эти потенциалы являются независимыми переменными, хотя и порождаются общей матрицей. Это видно уже из того, что в системе (48, 49) вследствие симметрии
– соответственно потенциалами общего электромагнитного и гравитационного полей. Заметим, что эти потенциалы являются независимыми переменными, хотя и порождаются общей матрицей. Это видно уже из того, что в системе (48, 49) вследствие симметрии 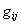 имеется
имеется 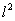 независимых уравнений при ранге матрицы
независимых уравнений при ранге матрицы 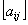 равном
равном 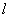 . Следовательно, задавая произвольно
. Следовательно, задавая произвольно 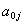 и
и 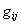 , получим систему уравнений, из которой можно найти
, получим систему уравнений, из которой можно найти 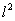 компонент матрицы общего поля. А это, в свою очередь, свидетельствует о принципиальной возможности существования такого поля. Независимость потенциалов
компонент матрицы общего поля. А это, в свою очередь, свидетельствует о принципиальной возможности существования такого поля. Независимость потенциалов 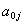 и
и 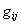 позволяет рассматривать общее поле в виде суперпозиции гравитационного и электромагнитного полей, выразив действие каждого из них через соответствующие потенциалы. При этом, варьируя потенциалы электромагнитного общего поля, можно игнорировать слагаемое действия
позволяет рассматривать общее поле в виде суперпозиции гравитационного и электромагнитного полей, выразив действие каждого из них через соответствующие потенциалы. При этом, варьируя потенциалы электромагнитного общего поля, можно игнорировать слагаемое действия 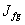 , а варьируя потенциалы гравитационного поля, можно игнорировать слагаемое действия
, а варьируя потенциалы гравитационного поля, можно игнорировать слагаемое действия 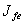 , что в значительной мере упрощает вывод и окончательный вид уравнений поля.
, что в значительной мере упрощает вывод и окончательный вид уравнений поля.
Для того, чтобы выразить действие самосогласованного поля, необходимо поставить ему в соответствие интеграл от скаляра, выраженного, в свою очередь, через соответствующие потенциалы и (или) их производные.
В классической теории электромагнитного поля [5] вид функционала 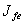 получают путём следующих рассуждений.
получают путём следующих рассуждений.
- Решение, в соответствие с общим принципом вариационных задач, ищется для класса допустимых полей, минимизирующих функционал вида
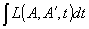 , т.е. содержащего в явном виде производные от потенциалов не выше первого порядка.
, т.е. содержащего в явном виде производные от потенциалов не выше первого порядка. - В выражение
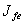 не могут входить потенциалы поля, так как они не определены однозначно вследствие калибровочной инвариантности вариационной задачи. Поэтому
не могут входить потенциалы поля, так как они не определены однозначно вследствие калибровочной инвариантности вариационной задачи. Поэтому 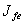 должен быть интегралом некоторой функции от тензора электромагнитного поля
должен быть интегралом некоторой функции от тензора электромагнитного поля 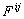 .
. - Функционал является скаляром и потому должен быть интегралом от скаляра.
- Электромагнитное поле подчиняется принципу суперпозиции: поле, создаваемое сложной подсистемой равно сумме полей, создаваемых каждой из входящих в неё подсистем. Математически этот принцип выражается в том, что тензор поля сложной подсистемы равен сумме тензоров, составляющих её подсистем. Следовательно, уравнения для поля должны быть линейными дифференциальными уравнениями. Из этого в свою очередь следует, что под знаком интеграла в функционале
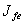
должно стоять выражение, квадратичное по полю. Только в этом случае уравнения будут линейными, так как при варьировании функционала степень подынтегрального выражения понижается на единицу.
Первые три пункта могут быть применены к абстрактному электромагнитному общему полю системы времени так как они лишь формализуют сущность вариационного метода. Четвёртый пункт в классической электродинамике постулируется в качестве эмпирического обобщения. В дедуктивной теории, базирующейся на гипотезе неодновременности, оснований для эмпирических обобщений нет, так как ею описывается абстрактное поле абстрактной системы относительно абстрактного наблюдателя. Тем не менее, именно гипотеза неодновременности даёт ключ к обоснованию четвёртого пункта без ссылок на физические эксперименты.
Как было показано выше, общее поле системы времени определяется матрицей 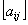 . Эта матрица ставит в соответствие траектории
. Эта матрица ставит в соответствие траектории 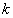 - той подсистемы во внутреннем пространстве некоторое распределение состояний
- той подсистемы во внутреннем пространстве некоторое распределение состояний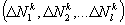 в цепи событий
в цепи событий 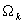 . Допустим, система времени
. Допустим, система времени 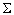 состоит из двух подсистем
состоит из двух подсистем  и
и 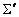 . При этом, согласно гипотезе неодновременности, множество её событий
. При этом, согласно гипотезе неодновременности, множество её событий 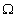 является объединением множеств событий подсистем
является объединением множеств событий подсистем 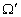 и
и 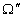 . Следовательно, множество
. Следовательно, множество 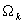 также может быть представлено объединением
также может быть представлено объединением 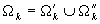 . Этому объединению соответствует равенство собственного времени
. Этому объединению соответствует равенство собственного времени 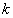 - той подсистемы в поле системы
- той подсистемы в поле системы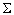 сумме собственных времён этой же подсистемы в полях подсистем
сумме собственных времён этой же подсистемы в полях подсистем  и
и 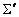 . Поля подсистем
. Поля подсистем  и
и 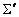 определяются матрицами
определяются матрицами 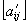 и
и 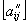 . Таким образом имеют место следующие равенства
. Таким образом имеют место следующие равенства
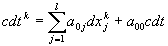 ,
,
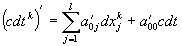 ,
,
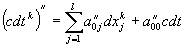 ,
,
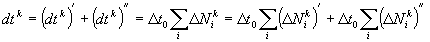 .
.
Эта система равенств имеет место лишь в том случае, если 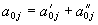 . Следовательно, электромагнитное поле системы времени подчиняется принципу суперпозиции.
. Следовательно, электромагнитное поле системы времени подчиняется принципу суперпозиции.
Заметим сразу, что гравитационное поле не подчиняется этому принципу уже в силу определения (49) его потенциалов. Вид функционала 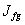 должен удовлетворять требованиям пунктов 1…3 и дополнительному условию, состоящему в том, что он должен тождественно обращаться в нуль при нулевой кривизне пространства событий. Эти условия выполняются в том случае если под знаком интеграла стоит скалярная кривизна
должен удовлетворять требованиям пунктов 1…3 и дополнительному условию, состоящему в том, что он должен тождественно обращаться в нуль при нулевой кривизне пространства событий. Эти условия выполняются в том случае если под знаком интеграла стоит скалярная кривизна 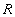 пространства событий. Хотя этот скаляр и содержит наряду с тензором
пространства событий. Хотя этот скаляр и содержит наряду с тензором 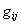 и его первыми производными ещё и вторые производные, но последние входят только линейно и вследствие этого не влияют на вариацию функционала
и его первыми производными ещё и вторые производные, но последние входят только линейно и вследствие этого не влияют на вариацию функционала 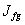 . Таким образом, на основании приведенных рассуждений приходим к выводу о том, что функционал общего поля системы времени, выраженный через потенциалы и их производные, должен иметь вид суммы действий для гравитационного и электромагнитного полей в искривлённом пространстве событий. Компилируя известные в электродинамике и общей теории относительности выражения, получим
. Таким образом, на основании приведенных рассуждений приходим к выводу о том, что функционал общего поля системы времени, выраженный через потенциалы и их производные, должен иметь вид суммы действий для гравитационного и электромагнитного полей в искривлённом пространстве событий. Компилируя известные в электродинамике и общей теории относительности выражения, получим
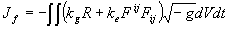 , (50)
, (50)
где 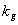 - гравитационная постоянная,
- гравитационная постоянная, 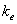 -постоянная электромагнитного поля,
-постоянная электромагнитного поля, 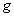 - определитель, составленный из величин
- определитель, составленный из величин 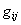 .
.
Объединяя функционал общего поля с ограничениями (37, 38), получим в окончательном виде функционал наиболее вероятной цепи событий
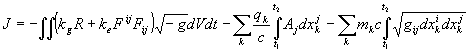 ,
,
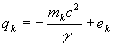 .
.
Варьируя этот функционал по траекториям, получаем уравнения движения; варьируя по потенциалам электромагнитного поля –обобщённые уравнения Максвелла для электромагнитного поля; варьируя по потенциалам гравитационного поля – уравнения Эйнштейна. Однако этих уравнений не достаточно для полного определения распределения и движения подсистем. Необходимо присоединить к ним ещё уравнения состояния системы времени, связывающие между собой термодинамические переменные. Эти уравнения нельзя получить варьированием функционала (47). И тем не менее, можно указать путь их вывода в виде следствий принципа наиболее вероятной цепи событий. Сравнивая (50) с (31), получим
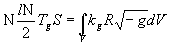 ,
,
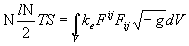 .
.
Исключая в этих уравнениях энтропию, получим уравнение, связывающее кривизну пространства событий с тензором электромагнитного поля и температурой системы
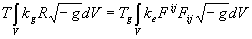 .
.
ЗАКЛЮЧЕНИЕ
Создание теории, объединяющей гравитацию и электромагнетизм – задача физики. Здесь же намечен общесистемный (спекулятивный, метафизический [2]) подход к этой проблеме. Я далёк от мысли, что выведенные соотношения окончательны и не потребуют пересмотра в дальнейшем. Тем не менее, как мне кажется, главное значение проделанной работы в том, что показана возможность построения абстрактной теории поля и уравнений движения абстрактной системы, исходя из представлений о конструкции необратимого “текущего” времени, а не изначально заданных геометрических свойств пространства, в котором времени отводится всего лишь роль одной из координат. Основная идея данной работы в том, что одно лишь Время как линейная необратимая упорядоченность абстрактных событий является причиной всех физических законов. Вспомним исходную постановку задачи. Рассматривается абстрактный автомат, взаимодействующий с внешней средой посредством сигналов, передаваемых с помощью бесконечной ленты, движущейся в одном направлении. Конечно же лента здесь является лишь удобной метафорой причинно-следственных отношений состояний автомата и внешней среды. Но вот что важно и является самым удивительным с моей точки зрения. Это абсолютная динамическая (энергетическая) независимость того внутреннего абстрактного мира, в котором существует автомат – наблюдатель от реального внешнего мира, где движение ленты требует механической работы, а автомат представляет собой нечто, называемое на сленге программистов “железом”. Хотя мы видели, что внутренний мир также как и внешний характеризуется силовыми полями, энергией, массами и зарядами подсистем – все эти величины ни каким образом не могут быть соотнесены с чем-то подобным во внешнем мире. Динамика внутреннего мира не зависит от того, какая энергия тратится на движение ленты, её физико-химических свойств и даже от того, движется она равномерно или нет. И, тем не менее, связь между мирами существует. Кинематика и динамика внутреннего мира обусловлена распределением состояний в цепи событий (символов на ленте). Следовательно, передавая информацию из внешнего мира, можно влиять на динамические процессы внутреннего, а сами эти процессы создают новую информацию во внешнем мире.
Задача исследования собственного мира абстрактной системы времени представляет интерес для науки (и прежде всего для темпорологии) даже в том случае, если окажется, что этот мир в чём-то отличается от наблюдаемого нами физического мира. Во всяком случае, в этой статье была сделана попытка доказать наличие формального подобия основных динамических законов, которые могут быть обнаружены наблюдателями этих миров.
ЛИТЕРАТУРА
- А. М. ЗАСЛАВСКИЙ. Геометрический образ внутреннего мира абстрактной динамической системы (интроспективный анализ и синтез временных рядов)
- А. М. ЗАСЛАВСКИЙ. Метафизика и системный анализ
- Р.КАЛМАН, П.ФАЛБ, М.АРБИБ. Очерки по математической теории систем. Перевод с английского. М.: Мир. 1971. 400с.
- К.ШЕННОН. Работы по теории информации и кибернетике. Перевод с английского. М.: Иностранная литература. 1963. 829с.
- ЛАНЛАУ Л.Д., ЛИФШИЦ Е.М. Теоретическая физика: Учебное пособие. В 10 т. Т. II. Теория поля. М.: Наука. 1988. 512с.
