Резюме  : Сначала я приведу неконструктивный аргумент, показывающий, что гипотеза механиста в когнитивной науке дает достаточно ограничений, чтобы решить, в чем может состоять «физическая реальность». Затем я объясню, как компьютерная наука вместе с логикой позволяет извлечь конструктивную версию аргумента, взяв интервью у скромной или Löbian Universal Machine. Обращая вероятностную интерпретацию квантовой логики фон Неймана на те, которые предоставляет машина Лёбяна, можно получить тестируемое объяснение того, как как физические законы, так и неинфекционные физические знания, то есть ощущения, возникают из числа теоретических соотношений.

 

Благодарность Спасибо моим друзьям, моим коллегам из IRIDIA и моим корреспондентам из Списка Всего и Списка Фактов о реальности за полезные и вдохновляющие обсуждения. Я несу полную ответственность за любую возможную ошибку или неловкость. Спасибо Бренде Лангедейк и Вальтеру Бельджерсу за приглашение на SANE 2004.

 

Вступление

Существует множество литературных источников, выступающих за или против гипотезы механиста, грубо говоря, идеи о том, что мы являемся машинами, и это задолго до и после Декарта Гоббс и их последователи выкупили в соответствии с так называемой современной (недавней) традицией.

 

Это не цель данной работы доводы ни механизма против. Вместо этого я предлагаю рассматривать это как рабочую гипотезу и искать ее логические последствия. Будет проще рассмотреть его более сильную цифровую версию хотя бы для того, чтобы получить точные определения, охватывающие различные научные дисциплины. Поступление таким образом в конечном итоге приведет нас к «чистым» научным вопросам в тестируемом Поппером смысле, в частности в форме математических и физических задач. Вполне разумно ожидать откровенного противоречия, и в этом случае мы получим «опровержение» цифрового механизма, но мы должны быть осторожны, чтобы не спутать противоречие с какой-то странностью [1] .

 

Определение:  Классический цифровой механизм, или Классический вычислительный механизм, или просто комп, - это совокупность следующих трех подгипотез:

1)       Гипотеза « да-доктор» : в когнитивной науке предполагается, что существует уровень описания моих частей (каким бы я себя ни считал[2] ), чтобы я не осознавал каких-либо эмпирических изменений в случай, когда выполняется функционально правильная цифровая замена моих частей на этом уровне. Мы называем этот уровень уровнем замещения. Проще говоря, это акт веры тех, кто желает сказать своему врачу « да» для искусственного мозга или искусственного пересадки тела, сделанного из некоторого описания на каком-то уровне. Мы увидим, что такой уровень непостижим. Обратите внимание, что некоторая часть народной или «бабушкиной психологии» неявно использовалась при предоставлении понятия (само) осознания [3] .

2)       Церковный тезис . Современная версия состоит в том, что все цифровые универсальные машины эквивалентны по классу функций (от натуральных чисел до натуральных чисел), которые они могут вычислять [4] . Можно показать, что это влечет за собой, что такие машины вычисляют одни и те же функции, но также они могут вычислять их сходными способами, то есть, следуя сходному алгоритму.Итак, в диссертации говорится, что, делая абстракцию времени вычислений, все цифровые универсальные машины могут точно симулировать друг друга (скажу, подражать друг другу).

3)       Арифметический реализм (AR). Это предположение, что арифметическое суждение, такое как «1 + 1 = 2», или гипотеза Гольдбаха, или отсутствие большего простого числа, или утверждение, что какая-то цифровая машина остановится, или любая булева формула, имеющая число, верны независимо друг от друга. от меня, вас, человечества, физической вселенной (если таковая существует) и т. д. Это версия платонизма, ограниченная по крайней мере арифметической истиной. Это не должно быть перепутано с намного более сильной пифагорейской формойАрканзас, Арканзас+, который утверждает, что вместе с их именуемыми отношениями существуют тольконатуральные числа: все остальные являются производными от этих отношений.

Чтобы сформулировать основные результаты, полезно заранее дать следующие определения, хотя более точные формулировки будут даны, естественно, в самой аргументации.

 

Определение Фундаментальная физика : я определяю ее с помощью рассуждения с правильным определением о наблюдаемом и проверяемом ожидании возможных относительно эволюционирующих величин и / или качеств.

У нас есть огромные эмпирические доказательства того, что квантовая механика является частью такой физики. [См. Cabello квази исчерпывающую и упорядоченную библиографию в архиве по адресуЛос Аламос  http://arxiv.org/abs/quant-ph/0012089 ].

 

Определение Фундаментальной машинной психологии : я определяю ее с помощью рассуждения правильного определения, которое машины могут иметь о себе или о других машинах. Это будет включать в себя, в частности, информатику, а также наборы предложений, которые некоторые машины могли бы правильно утверждать о себе (называемые самореференциально правильными дискурсами).

 

Нет ничего нормативного в использовании слова «правильный»:   если мы когда-либо знали, что причина появления луны в небе состоит в том, что 667 маленьких ангелов толкают ее туда, то это было бы правильным объяснением по определению. Нам не нужно уточнять: в конце концов, слово «правильный» будет просто означать арифметически истинное. Это должно быть прояснено через рассуждения, которые последуют.

Статья состоит из двух частей:

Часть 1 представляет неформальный, но (мы надеемся) строгий аргумент или доказательство, названное Универсальным аргументом доводчика (UDA), в форме последовательности из восьми мысленных опытов [5] , показывающих, что из comp следует, что фундаментальная физика обязательно сводится к фундаментальная психология. Обратите внимание, что с помощью comp можно легко показать, что фундаментальная психология встраивается в теорию чисел [6] . 

Часть 2 , благодаря многочисленным открытиям Геделя, Церкви, Тьюринга, Поста, Маркова и многих других (главным образом, исследований Брауэра, Хейтинга, Лёба, Гжегорчика, Боулоса, Гольдблатта, Кузнецова, Муравицкого, Соловая, Виссера) в исследовании «Я» и в «Арифметической самореференции» объяснят, как взять интервью у Самореференциально-правильной универсальной машины (SRC-машины) по заключению УДА для выработки некоторой логики физических утверждений. Затем мы сравним эту логику с эмпирической логикой физических утверждений, которые были выведены из наблюдений. Это покажет, что comp является тестируемым и даже что некоторый тест уже подтверждает это (и это , конечно, не означает, что это доказывает ). Прежде чем обратиться к доказательству изменения психологии / физики и его математическому подтверждению, позвольте мне предупредить разумного человека, что оба могут вызвать некоторое количество метафизического головокружения [7] .

 

I. Аргумент универсального доводчика показывает, почему comp обязательно вызывает изменение между физикой и психологией машины

Здесь представлен аргумент, показывающий, что если мы достаточно серьезно относимся к вычислительной гипотезе в когнитивной науке, то физика сводится к машинной психологии. Доказательство разделено на 8 шагов. Каждый шаг пронумерован и сопровождается рисунком, показывающим основную идею шага.

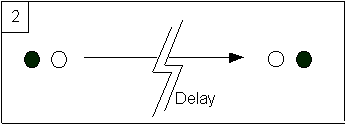
            1) Comp делает возможным (только в принципе, но это все, что нам нужно) использование классической [8] телепортации. Вы читаете и режете, с обычным значением компьютерной практики, вБрюссель, Мы предполагаем, что чтение было сделано, возможно, случайно, на уровне, равном или ниже, чем уровень замещения.   Отсканированная (прочитанная) информация отправляется традиционными средствами, например, по почте или по радио, наХельсинкигде вы правильно воссозданы с окружающей органического материала. «Правильно» по определению комп. Обратите внимание, что мы не делаем вид, что врач точно знает правильный уровень замещения. Собственно комп сделает такие знания обязательно невозможными. Но комп говорит, что уровень существует, и мы предположим, что доктор сделал ставку на правильном уровне.

 

 

На рисунке телепортированный человек представлен черным ящиком. Его уничтожение представлено белой рамкой, появляющейся слева от стрелки. Восстановление представлено белой рамкой справа от стрелки. Если мы идентифицируем человека с его (мы надеемся, последовательным) набором убеждений, опыт добавляет только новое убеждение (я действительно прибыл вХельсинки) к набору, и результирующий набор можно рассматривать как последовательное расширение набора до телепортации.

2) Шаг и рисунок 1 являются лишь подтверждением гипотезы компа. Для продолжения необходимо ввести ключевое различие между понятиями от первого лица и от третьего лица. В самом аргументе будет достаточно определить их пропозициональным содержанием личных дневников. Точка зрения третьего лица - это содержание описания эксперимента внешним наблюдателем, который не участвует в телепортации. Точка зрения первого лица - это содержание дневника, снятого пользователем устройства телепортации. Он должен взять его с собой, чтобы личный дневник сам был уничтожен и восстановлен. Чтобы облегчить рассуждение, мы пренебрегаем первым чтением ивставкой времени, поскольку пренебрегаем путешествием во времени описательной информации. В этом простом эксперименте / опыте по телепортации нет разницы между дискурсом от первого и третьего лица, учитывая, что в обоих дневниках описывается кто-то изБрюссель вХельсинки, Некоторые местоимения могут отличаться, но они имеют сходные ссылки, и они не более двусмысленны, чем в их традиционном обычном понимании бабушки. На втором шаге появится разница между видом 1 и видом 3. Это эксперимент по телепортации, когда восстановление или, что то же самое, путешествие было отложено на один год (скажем).

 

 

 

 

 

 

Учитывая, что мы принимаем comp, «опытный» не имеет возможности, если он лишен каких-либо внешних ключей (окно восстановления не имеет окна и т. Д.), Что-либо узнать об этой задержке. Его дневник не будет и не может упомянуть его, так что речь первого человека такая же, как в предыдущем эксперименте. Наоборот, в дневнике внешнего наблюдателя будет упоминаться об этой очень большой задержке. На втором этапе дискурсы первого и третьего лица больше не совпадают.

 

 

 

3) третий шаг по общему признанию интригует; его последствия не меньше. Описание закодировано вБрюссельпосле процесса чтения-вырезания это просто описание состояния некоторой машины Тьюринга [9] , давая, что мы предполагаем комп. Таким образом, его описание может быть продублировано, и опытный специалист может быть восстановлен одновременно в двух разных местах, напримерВашингтон иМосква, Восстановление вМосква не зависит от восстановления в Вашингтони comp делает переживающего пережившим этот эксперимент двойной телепортации. ВБрюссельдо продолжения эксперимента экспериментатор не может дать аргументацию о том, что он не выжил вВашингтонтак что «найти себя в Вашингтон»Дает последовательное продолжение. Те же рассуждения показывают, что «найти себя вМосква”Является альтернативным последовательным расширением. Давайте спросим опытного, который должен быть практикующим специалистом, где он будет находиться после эксперимента. Он может ответить от третьего лица , сказав, например, что если кто-то захочет позвонить ему, он присоединится к обоим поМосква и вВашингтон, Итак, давайте спросим его более искренне, где он будет чувствовать себя после дублирования, то есть того, что будет написано в его личном дневнике. Дневники дублируются, и, очевидно, ни один из них не будет содержать высказывание «Я чувствую, чтоВашингтон и Москва«. Тот, кто чувствует, что его восстановили в Вашингтоне, может иметь только интеллектуальное (3 человека) убеждение, что он также был восстановлен в Москве (соответственно, в Вашингтоне), но даже в этом он не может быть уверен без внешних подсказок, таких как телефон или видео подтверждение. С его позиции другая личность выглядит как другая , как близнец, падающий с неба.

 

 

 

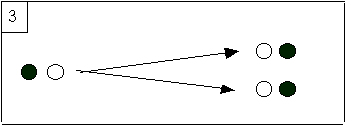Поэтому после эксперимента каждый «первый человек» будет чувствовать себя в одном месте. Быть в обоих местах никогда не будет осуществимым последовательным убеждением с точки зрения первого лица. Предоставляя встроенную симметрию этого эксперимента, если его спросить перед экспериментом о его личном будущем местоположении, опытный специалист должен признать, что он не может с уверенностью предсказать личный результат эксперимента. Он сталкивается с неизбежной неопределенностью. Это замечательно, потому что с точки зрения третьего лица эксперимент является полностью детерминированным, и действительно, доктрина механистов защищает большую часть времени сторонниками детерминизма. Но мы видим здесь, что механизм, будучи действительно полностью 3-детерминированным, влечет за собой сильную форму неопределенности [10] , имеющую отношение к возможным последовательным расширениям, когда они наблюдаются от первого лица, как могут наблюдать оба дневника. Это то, что я называю неопределенностью первого лица , или просто неопределенностью 1. Давая этоМосква и Вашингтон являются перестановочными без каких-либо заметных изменений для опытного, разумно отнести вероятность ½ к событию «Я буду в Москва (Соотв. Вашингтон) «. Прежде чем продолжить, испытатель находится в состоянии максимального невежества.На самом деле, мы делаем этот шаг только для упрощения презентации. Действительно, в конечном итоге мы сведем физику к поиску меры неопределенности для 1-неопределенности, и на этом этапе это также может быть мерой достоверности . Тем не менее, в настоящем контексте такая вероятность может быть интуитивно обоснована как с помощью определения вероятности в ставках, так и с помощью частотного подхода к вероятности посредством итерации экспериментов. В обоих этих случаях мы должны учитывать дублирование не отдельного человека, а совокупности лиц. Это приводит к понятию множественного числа от первого лица, где вероятности и ставки являются локально передаваемыми. Например, люди внутри каждой умноженной популяции могут оценить эти вероятности и оценить справедливость ставок, связанных с дублированием. С локальной точки зрения, разделяемой человеком, принадлежащим к дублированным группам, 1-неопределенность выглядит как неопределенность от третьего лица, но это так только внутри каждой группы.

 

            4) Четвертый шаг показывает, что вызванная симметрия и одновременность были красным ошибочным оправданием.   Для этого достаточно ввести в предыдущей настройке задержку восстановления в одной из разветвляющихся ветвей. Тогда мы можем использовать факт, установленный на втором этапе, что человек с его внутренней первой личной точки зрения не может знать о задержке, чтобы понять, что введение асимметричных задержек не изменит перспективу от первого лица. Хотя точная мера неопределенности от первого лица не была (и никогда не будет) определена точно, ключевой момент заключается в том, что такая мера не изменяется при таких задержках. В частности,если бы мы так решили приписать вероятность ½ на последовательных расширений на шаге 3, то мы должны приписать вероятность ½ в асимметричном дублирования, и это точка , мы хотели показать.

 

 

 

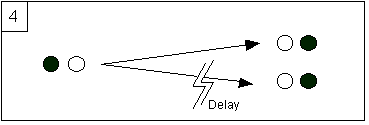5) До сих пор тот, который мы могли условно назвать «оригиналом», всегда уничтожался в Брюссель, его отправная точка. Что можно сказать о вероятности достиженияАмстердам из Брюссельс простой телепортацией, когда оригинал не уничтожен вБрюссель, На рисунке пять изображен эксперимент:

 

 

 

 

 

Отсутствие белого пятна слева означает, что в начальной точке аннигиляции нет. Также можно учесть, что на стрелке есть естественная неявная задержка. Это является следствием предыдущих шагов, что если вероятность равна 1/2 на шаге 3 (и, следовательно, также на шаге 4), она должна быть 1/2 на шаге 5. Причина в том, что эта установка может быть пересмотрена эквивалентно как дублирование-телепортация ( как в шаге 4) изБрюссель к {Брюссель, Амстердам} с нулевой задержкой восстановления вБрюссель, Это, конечно, нелогично [11] , особенно если неявная задержка велика, потому что приБрюссель, это только картинка, которая была сделана (очень точная, показывающая, что она была сделана на правильном уровне замещения (который существует в comp)), и почему мы должны бояться картины самого себя? Конечно, если кто-то делает этот опыт в состоянии быть уверенным, он появится вБрюссельодин в Амстердампоймет ложь, но никогда не сможет убедить «оригинал» в ее ошибке. И это показывает, кстати, что ни один из представленных опыта / эксперимента никогда не может считаться доказательством сложной гипотезы. На самом деле, таких доказательств не может быть, поскольку читатель, возможно, разработает его сам.

 

6) Шестой шаг сродни древнейшему метафизическому аргументу. Это также самый многолетний и универсальный, это обсуждается в старых индусских, буддистских, даосских, исламских, еврейских и христианских текстах. Он играет роль в Театете Платона, в «Размышлениях Декарта» и во многих других. В своей форме он используется во многих фантастических романах; как Simulacron III от Daniel Galouye, или в фильмах, как The Matrix . Это аргумент мечты , и он показывает, главным образом, что мы всегда можем ошибочно принять простую веру в знания. Мы увидим, как звуковая универсальная машина будет отражать эту проницательность в своих самореференциально правильных дискурсах, но на этом этапе все, что нам нужно, сводится только к следующему следствию comp: все предыдущие шаги могут быть выполнены снова с восстановлением, являющимся « виртуальный », т. е. эмулируемый универсальной машиной,   а не« реальный », и это без какого-либо возможного изменения в опыте первого лица в течение некоторого произвольного конечного времени, связанного с точностью воспроизведения сред (например, в Вашингтоне и Москве). ). Все, что вам нужно, это смоделировать правильный интерфейс, который является эмулируемым по Тьюрингу, по определению comp, и тогда какое-то приближение среды будет успешным, чем мельче описательные детали, тем дольше будет время. Комп позволяет заменять сны видеоиграми в аргументе о старом сне в том смысле, что первый человек не может отличить «реальность» от ее эмуляции, когда это делается на уровне ниже уровня замещения.

 

           

 

 

На рисунке 6 прямоугольник представляет (конечный) вычислительный механизм. Здесь важно то, что какую бы меру неопределенности comp 1 мы не выбрали, эта мера не изменится в случае, когда восстановление является виртуальным. Даже если симуляция не длится долго, каждый первый человек примет любую личную реконструкцию как подтверждение своего ожидания, то есть ставок на его последовательные расширения. Вероятностное исчисление снова инвариантно для такого изменения. Это непосредственно следует из нашего предыдущего предположения о том, что существует правильный уровень замещения и что мы эмулируемы по Тьюрингу.

 

7) Седьмой шаг знакомит с универсальным голубятней (UD). Пусть N обозначает множество натуральных чисел. Функция от N до N называется полной, если она определена на всех натуральных числах. Функция называется вычислимой, если существует программа FORTRAN, которая ее вычисляет [12] . Церковный тезис (КТ) делает особый выбор ФОРТРАНА неуместным. CT утверждает, что все вычисляемые функции, суммарные или нет, вычисляются по алгоритму, выражаемому в FORTRAN. В частности, все общие вычислимые функции вычисляются с помощью такой программы FORTRAN.

            По словам Т-Фортрана, существует ли язык, способный определять все и только все общие вычислимые функции? Язык T-Fortran, с некоторыми четко определенными грамматическими ограничениями, может создавать любые написанные на нем алгоритмы, вычисляя только полные функции.   Ответ - нет." Если бы это было так, мы могли бы перечислить программы T-Fortran по лексикографическому порядку: P ₁ , P ₂ , P ₃ …   и следующая функция g, определенная для n с помощью P _n (n) +1, была бы вычислимой , но не вычислимый T-Fortran. В самом деле, существует программа T-Fortran P _k, вычисляющая ее, тогда P _k (k) = P _k (k) + 1, и это абсурдно, если считать, что P _k (n) является четко определенным числом для каждого n (потому что функция полная). Таким образом, с тезисом Черча, набор программ, вычисляющий полные функции, обязательно является надлежащим подмножеством набора программ, вычисляющих функции, написанные на Фортране. Сам Фортран вакцинирован от предыдущей диагональной «атаки». Действительно, хотя мы можем перечислить все программы на Фортране (и это можно сделать механически), и хотя получающаяся в результате диагональная функция g может быть запрограммирована на Фортране, и она будет в своем коде снова давать g (k) = g (k) + 1, мы не получим противоречия, а только, на жаргоне информатики, сбой компьютера, то есть вычисление g (k) будет выполняться вечно. И это влечет за собой то, что не существует полной и разрешимой теории, способной решить из описания программы, вычисляет ли она общую или неполную функцию, потому что в этом случае мы сможем использовать эту теорию для механической фильтрации неполных программ и получить с CT - перечисление всех и только всех вычисляемых функций; но тогда мы снова получим противоречие, которое мы получили выше. Это показывает, что неполнота теорий относительно истины является прямым следствием КТ. Абсолютность вычислимости, гарантированная КТ, делает неизбежным относительность теорий. Это снова будет отражено в нашем универсальном машинном интервью. Что касается данной стадии в рассуждениях, это объясняет , почему , если мы хотим построить универсальную машину, которая не только способна эмулировать все машины, но которые на самом деле делает эмуляцию каждой машины, мы будем обязаны ласточкин хвост на каждом исполнении. Мы должны сгенерировать все программы на Фортране, P ₁ , P ₂ , P ₃ ..., и выполнять их небольшими частями, возвращаясь периодически во всех программах. Пусть P _i ^j (n) представляет j шагов выполнения i- ^йпрограммы P _i на входе n. Мы просто должны вычислить все эти P _i ^j (n), и это легко, потому что тройка <i, j, n> алгоритмически перечислима.Это можно рассматривать как способ эмулировать цифровой параллелизм линейным последовательным образом. Этот способ позволяет избежать риска никогда не останавливаться на возможном бесконечном вычислении из-за необходимости существования неостанавливаемых программ, как мы только что показали. Такая процедура называется процедурой «ласточкин хвост», и я называю универсальную машину, которая подходит для всех возможных машинных исполнений, универсальным голубятником (UD). Предположим теперь, ради аргумента, что наша конкретная и «физическая» вселенная является достаточно мощной расширяющейся вселенной, так что «конкретный» UD может работать вечно, как показано на рисунке 7.

 

 

 

 

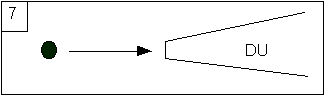Затем из шести предыдущих шагов следует, что он будет генерировать все возможные состояния машины Тьюринга, бесконечно часто (почему?), Которые (по данным comp) включают в себя все ваши виртуальные восстановления, соответствующие (надеюсь) последовательным расширениям себя, во всех возможных ( локально) эмулируемые среды или истории вычислений. И это, с компом, даже в том случае, если вы считаете, что ваш «обобщенный мозг» («все», что необходимо для эмуляции цифрового тела / мозга, чтобы выжить) - это целая галактика Млечного Пути. И нам не нужны никакие устройства, подобные научной фантастике, чтобы сделать этот бетон [13] , если мы сделаем исключение из надежной вселенной.

Мы почти закончили. Действительно, давайте попробуем простой «физический эксперимент», например, бросить ручку. С comp, когда мы находимся в состоянии уронить перо, мы находимся в эмулируемом состоянии Тьюринга. Наше более вероятное непротиворечивое расширение не определено неопределенностью в 1 комп во всех «воссозданиях» подобных состояний, появляющихся в UD * (бесконечный след UD). Это следует из 6, и инвариантности меры неопределенности, в частности, для произвольной задержки, включая нулевую, и бесконечного набора состояний, появляющихся с произвольно большой задержкой в ​​работе УД [14] . Это дает огромный набор. Можно утверждать, что конечные вычисления имеют нулевую меру, и что единственный путь к мере на состояниях состоит в том, чтобы найти меру на множестве максимально полной истории вычислений, проходящей через эти состояния, с очевидно, довольно трудно определить эквивалентность соотношение между вычислениями. Тем не менее, мы можем показать, что эти (бесконечные) вычисления, как видно из описания UD * от третьего лица, соответствуют максимально согласованным расширениям наших (мы надеемся) реальных согласованных состояний. Здесь нет необходимости быть более точным, учитывая неконструктивизм набора этих непротиворечивых расширений и тот факт, что мы сделаем вещи совершенно точными, непосредственно опросив универсальную машину по этим расширениям, и это с учетом Различия с точки зрения 1/3 человека. Итак, если мы предоставим достаточно устойчивую вселенную, мы полностью закончили: физика, как «правильная» наука для конкретных относительных предсказаний, должна быть дана какой-то мерой относительно наших последовательных относительных состояний.Физика, в принципе, сводится к оценке совокупности вычислительных историй, как видно с точки зрения первого лица. Можно сказать, что в принципе физика была сведена к фундаментальной компьютерной психологии.

 

            8) Да, но что если мы не предоставим конкретную здоровую физическую вселенную? До этой стадии мы все еще можем избежать завершения семи предыдущих шагов рассуждения, утверждая, что «физическая вселенная» действительно «существует» и слишком мала в смысле неспособности генерировать весь UD * или какой-либо другой. разумные части этого, так что наши обычные физические предсказания были бы защищены от любого вмешательства в его «маленькие» вычислительные истории, порожденные UD.    Такой шаг можно рассматривать как случайный и позорный. Это также может быть довольно ослаблено некоторым принятием некоторой концептуальной версии бритвы Оккама, и, очевидно, этот шаг не имеет цели для тех, кто готов принять comp + (в этом случае UDA просто показывает необходимость обхода в психологии, и общая форма физики как усреднение по последовательной 1-истории ). Но, по логике вещей, все еще есть место и для физикализма, и для компа, когда мы сделали этот шаг. На самом деле 8- ^й настоящий шаг объяснит, что такой шаг, тем не менее, не имеет смысла. Это сделает представление о конкретной и существующей вселенной полностью лишенным какой-либо объяснительной силы. Из этого следует, что гораздо более слабая и обычная форма бритвы Оккама может быть использована для заключения о том, что не только физика эпистемологически сведена к машинной психологии, но и что «материя» онтологически сведена к «уму», где разум определяется как объект изучение фундаментальной машинной психологии. Все это, принимая комп, я настаиваю. Причина в том, что комп запрещает связывать внутренний опыт с физической обработкой, связанной с вычислениями, соответствующими (с компом) этим событиям. Физический «тезис супервентности» философов разума материалистов не может быть поддержан, а внутренний опыт может быть связан только с типом вычислений.

Вместо того, чтобы связывать [боль, которую я чувствую] в пространстве-времени (x, t), с [состоянием машины] в пространстве-времени (x, t), мы обязаны связать [боль, которую я чувствую в пространстве-времени (x , t)] к типу или пучку вычислений (существующий навсегда в арифметической Платонии, который считается существующим независимо от нас самих с арифметическим реализмом). Этот результат был найден независимо мной и Тимом Модлином (Marchal 1988, Maudlin 1989). Аргументация Модлина дает больше информации[15] . Аргумент менее понятен, чем аргументы предыдущего шага, и я лишь обрисую лишь основной принцип.

Для любого конкретного точного вычисления, связанного с каким-то внутренним опытом, вы можете модифицировать устройство таким образом, чтобы количество задействованной физической активности было произвольно низким и даже нулевым для опыта сновидения, у которого нет входов и выходов. Теперь, подавив физическую активность, присутствующую в текущих вычислениях, машина будет толькослучайно исправлена. Это будет правильно только для этого точного вычисления с неизменной средой.   Если это немного изменить, это сделает компьютер, выполняющий вычисления, более не корректным. Но затем Модлин со всей очевидностью показал, что контрфактическая корректность может быть восстановлена ​​путем добавления неактивных устройств, которые будут срабатывать только в том случае, если в окружающей среде появятся некоторые (контрфактуальные) изменения. Теперь это показывает, что любой внутренний опыт может быть связан с произвольно низкой (даже нулевой) физической активностью, и это в сохранении контрфактической правильности. И это абсурдно в сочетании компа и материализма.

Так что, если мы будем держать комп на этом этапе, мы вынуждены связывать внутренний опыт только с типом вычислений. Причина в том, что только эти типы однозначно связаны со всеми их возможными контрафактами.   Это влечет за собой то, что, с точки зрения первого лица, не только физическое невозможно отличить от виртуального, но виртуальное больше нельзя отличить от арифметического [16] . Теперь DU эмулируется платонистически проверяемыми предложениями арифметики. Они эквивалентны предложениям вида «существует n такое, что P (n)» с разрешимостью P (n). Их истина влечет за собой их доказуемость, и они известны под названием предложения Сигма1.

Если комп верен, появление физики должно быть восстановлено с некоторых точек зрения, вытекающих из этих положений. В самом деле, еще раз принимая во внимание семь шагов, мы приходим к выводу, что физическое атомное (в логическом смысле) инвариантное предложение должно быть задано вероятностной мерой на этих предложениях. Физическая уверенность должна быть истинной во всех максимальных расширениях, истинной по крайней мере в одном максимальном расширении (мы увидим позже, почему второе условие не следует из первого) и доступной для UD, что является арифметически проверяемой.   Рисунок 8 иллюстрирует наш главный вывод, где число 1 ставится для так называемых Sigma1 предложений арифметики.

 

 

 

 

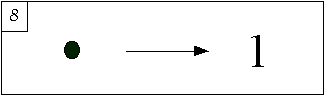Вывод : физика определяется мерой последовательных вычислительных историй или максимальных последовательных расширений, как видно с некоторой точки зрения от первого лица. В частности, законы физики должны быть выведены из истинно проверяемых «атомных предложений». Это проверяемые арифметические предложения. Они должны быть истинными везде (= во всех историях обработки), истинными где-то (= истинными по крайней мере в одной истории обработки) и выводиться из доступных для DU «атомарных» состояний [17] .

 

II. Интервью « Скромная машина» дает нетривиальный зародыш подтверждения Comp в форме арифметической квантовой логики

Чтобы оценить comp по его, возможно, поразительным последствиям, мы примем поразительно наивную методологию: мы будем опрашивать саму машину. Учитывая, что рассуждения UDA показали, что физика должна возникать из вероятностной структуры, опирающейся на ее максимально согласованные расширения; естественно опросить машину на предмет ее последовательных расширений. Очевидно, что допросить произвольную машину не обязательно будет интересно. В конце концов мы будем опрашивать само-референсную, арифметическую платонистскую универсальную машину Тьюринга (SRC-машину), и это в кадре вычислителей. Точность будет следовать. На первый взгляд такой выбор может создать ощущение, что мы начинаем задавать вопрос, давая нам возможность взять интервью у машины, которая «разделяет» наши гипотезы. Но это нормально, если мы будем спорить ни за, ни против комп. Мы просто изучаем, как и в первой части, логические последствия комп. Очевидно, что на данном этапе мы можем только надеяться, что машина сможет дать более точную информацию, чем неофициальные (но точные) последствия, которые уже дают неконструктивные рассуждения UDA [18] .

Наивная методология предлагает нам занять наивную позицию по отношению к убеждениям машины. Это означает, что мы будем говорить, что машина верит предложению p тогда и только тогда, когда машина утверждает p. Мы должны выбрать [19] достаточно болтливую машину, способную отстаивать любые свои убеждения или оценивать их так или иначе, когда их об этом спрашивают. Мы должны выбрать достаточно серьезную машину. Например, нет реальной проблемы с машиной, утверждающей, чтоЛондон это столица Франция, Мы все еще можем быть снисходительными к машине, просто приписывая ее отсутствию знакомства с элементарной географией. Но если машина утверждает, чтоЛондон не столицаФранция и утверждает, чтоЛондон это столицаФранциятогда это заставило бы нас подозревать, что убеждения машины, скорее всего, противоречивы, особенно если машина была представлена ​​как машина Платониста.

 

Презентация машины.   О машине говорят « платоник» или « Классика» , если 1) машина верит всем классическим тавтологиям, и 2) это тот случай, когда машина верит в X и верит в X -> Y, тогда машина будет верить в Y. I скажет, что машина последовательна, если ее набор убеждений не содержит противоречия. f (читается как false) сокращает любое противоречие, например (p & -p), где p обозначает некоторое предложение. Я напишу Bp как аббревиатуру для предложения, согласно которому машина считает p. В случае, если мы добавим предложение p к согласованному набору мнений машины, мы скажем, что машина остается последовательной, если машина не получает противоречие из p.Таким образом, p будет согласовано для машины, если -B- p, т. Е. Утверждение -B- p верно, т.е. машина не доказывает отрицание p. Таким образом, мы можем прочитать -B- как последовательный . Например, -B- -p говорит, что -p непротиворечива, и это эквивалентно неправдоподобности p, то есть -Bp. Понятие логических следствий конечного множества высказываний определяется обычным образом [20] .Машина будет названа арифметическим платоником, если машина верит достаточно элементарной арифметической истине (включая некоторую схему аксиомы индукции). Машина будет самореференциально правильной или самоточной, когда любое утверждение, которое машина когда-либо верит в отношении своих собственных убеждений или утверждений согласованности, является правильным, и это, например, когда B переводится или кодируется каким-либо образом на его языке, например арифметика. Машина будет называтьсяуниверсальной , если она способна эмулировать любые вычисления. Чтобы быть универсальным, достаточно, для классической арифметической платонической машины, верить всем истинным предложениям Sigma1. Я вспоминаю, что они имеют форму «существует n такое, что P (n)». С аксиомами индукции у такой машины будет достаточно интроспективной силы, чтобы «знать» (в смысле «правильно верить»), что существуют универсальные; в том смысле, что они поверят p -> Bp для любого арифметического предложения Sigma1. Это в конечном итоге предоставит нам очень простой способ перевести гипотезу вычислителя на машинный язык, добавив убеждение p-> Bp к убеждениям машины, отождествив атомное убеждение с понятием доступности DU.

 

Тот факт, что мы просим перевести «B» на машинный язык, то есть в терминах объекта, с которым машина способна справиться, подобно числам, делает машинные убеждения «научными», то есть передаваемыми (утверждаемыми) убеждениями от третьего лица. Это также защищает нас от обвинений Куайна в эссенциализме. Машина говорит о каком-то описании себя, как опытный человек говорит от третьего лица внешним образом об описании своего тела с хирургом или о своем двойнике после эксперимента с самовоспроизведением.   Это означает, что нам нужно определить на машинном языке понятие точек зрения от первого лица. Это будет сделано позже, используя традиционное определение, данное Theaetetus Сократу, и варианты в Theaetetus Платона.

 

Гёдель, Умы и Машины. Известно, и мы увидим, почему ниже, что все машины страдают от некоторых внутренних ограничений, которые связаны, в частности, с различием, обнаруженным Геделем [21] , между правдой и доказуемостью. Важная литература касается влияния результатов Гёделя, ограничения формальных систем на вопрос о механизме. Есть те, кто, как Лукас и Пенроуз, думают, что неполнота Геделиана показывает, что мы не машины, те, кто сомневается в каких-либо положительных или отрицательных отношениях, и те, кто верит и утверждает, что теорема Геделя действительно является шансом для механизма. Мы, как и Джадсон Уэбб, квази по построению относимся к этой последней категории. Полагая, что неполнота является прямым следствием тезиса Черча, как мы показали, и подтверждая, что Гедель доказал свою теорему неполноты без КТ, Джадсон Уэбб в замечательной книге заключает, что неполнота не могла быть более удачным открытием для механиста : это подтверждение КТ. И это делает CT вакциной, которая защищает универсальные машины от неправильной диагонализации. В конце концов это защищает бабушку от теории господина! 

Насколько мне известно, ни один логик не убедил Лукаса или Пенроуза использовать результаты Геделя против механизма [22] . Были предложены некоторые подлинные реконструкции аргумента Лукаса, и существует консенсус, что неполноту можно использовать, чтобы показать, что, если мы являемся последовательными машинами, то мы не можем знать, какой мы станем, и тем более, в какой истории вычислений мы, скорее всего, поддерживаемся! [23] Даже Пенроуз признает этот фундаментальный нюанс в своей второй книге бестселлеров по этому вопросу, но, как ни странно, не принимает во внимание этот нюанс. 

На первый взгляд, UDA, которое вынуждает нас фиксировать физику с помощью меры на последовательных расширениях машины SRC, может привести к некоторому противоречию со второй теоремой о неполноте (которая будет доказана ниже). Это говорит о том, что машина SRC не может поверить в свою непротиворечивость, -B (-Bf) верно для такой машины, поэтому,   если вы спросите такую ​​машину, есть ли у нее (хотя бы) одно последовательное расширение, она будет молчать! И без всякой осторожности машина просто снова разбилась! К счастью, если мы проявим терпение и позволим машине SRC согласовать свои убеждения с оправданиями, рано или поздно она «объяснит» свое молчание, заявив, что -Bf   -> -B-Bf, то есть машина считает, что если она последовательна, то она не могу поверить в его последовательность.

            Первым открытием Геделя было то, что любая машина, способная доказывать арифметические теоремы, либо доказывает ложности, либо неспособна доказать какое-либо истинное арифметическое утверждение. Урок в том, что какую бы машину мы ни выбрали;правда всегда будет правильно расширять свои формальные (разделяемые, проверяемые) способности доказуемости. Но как опросить машину по геометрии ее незнания, как это определено ее набором последовательных расширений, если машина так ограничена.   Теоретически более короткий путь к решению будет предложен в форме пары логик самоссылки, логики доказуемости Соловея G и G *, которые можно считать плодотворным и удивительным потомком эпохи Гёделя и Лёба, делающей неполноту теоремы. Сейчас я попытаюсь, позаимствовав уловку из мягкого введения Смулляна в незавершенность, изложить основные идеи, не вдаваясь в слишком много технических деталей. Я вряд ли могу дать лучшую рекомендацию, чем пригласить тех, кто хочет немного ознакомиться с понятиями, которые здесь используются, для изучения прекрасной книги Смулляна.

 

Смуллян Педагогика . Для объяснения теорем Геделя и Лёба [24] Смуллян предлагает загадку. Есть остров, на котором все местные жители - рыцарь или мошенник. Рыцари всегда говорят правду, а мошенники всегда лгут. Какой-то разум посещает остров, а один житель говорит ему: «Ты никогда не узнаешь, что я рыцарь». Что мы можем вывести [25] ?

Мозгец мог рассуждать следующим образом. Давайте предположим, что уроженец мошенник. Тогда он лгал, а это значит, я буду знать, что он рыцарь. Но я не могу знать, что он рыцарь, когда он мошенник, поэтому он не может быть мошенником, и, соответственно, он рыцарь.Теперь мы можем вести противоречие. Мы знаем, что мыслитель рассуждал правильно, поэтому натив действительно рыцарь, и он полагает, что натив рыцарь. Итак, мы знаем, что мыслитель знает, что это рыцарь, но тогда туземец ошибался и должен был быть мошенником, и это противоречие. Зная, что мы имели в виду правильно верить. У нас есть парадокс! Очевидно, это вариант парадокса Эпименида. Теперь, чтобы позволить самому мыслителю сделать такой парадоксальный вывод, мы должны предположить некоторую способность рассуждать.Действительно, как искренне объясняет Смуллян, никакого парадокса не возникнет в случае, если житель скажет трупу или, в меньшей степени, глухому: «Вы никогда не узнаете, что я рыцарь». Действительно, в этом случае житель - рыцарь, и глухой этого не узнает, учитывая, что он даже не слышит вопроса. Если вы умственно отсталый, никакого парадокса тоже не возникает. Некоторые туземцы говорят вам одно и то же предложение, и вы можете ответить «Ах, хорошо», ничего не выводя, и никакого парадокса не произойдет. Так каковы минимальные умственные способности, чтобы получить парадокс? Для этой проблемы можно показать, что знания классической логики высказываний достаточно вместе с предположением, что рассуждатель нормален , то есть, если он знает p, то он знает, что он знает p.

Рассуждение показало, что в случае существования такого острова ни один абориген никогда не скажет обычному знатоку классической логики: «Вы никогда не узнаете, что я рыцарь». Это приводит мыслителя к откровенному противоречию. Конечно, это также может означать, что «туземец» не был туземцем, это мог быть шутливый турист или безумный исследователь, замаскированный под мошенника.

            Теперь предположим, что (настоящий) уроженец говорит вам вместо этого: «Вы никогда не поверите, что я рыцарь». Что вы можете вывести? Мы неукоснительно следовали традиции, которая берет свое начало в «Театете Платона», определяя знание некоторого предложения р правильной верой в это утверждение. То есть, по определению, «зная p» - это «верить p» с p true. Мы можем написать Cp = p & Bp, где Cp означает (когда-либо) знать p, а Bp означает (когда-либо) поверить p.

 Переход от знания к вере делает вещи более тонкими и интересными. Действительно, приведенный выше парадокс, например, произойдет, только если посетитель (к которому обращается житель) верит, что все его убеждения верны. В случае, когда все его верования действительно верны, приведенные выше рассуждения покажут, что мыслитель не может ни поверить, ни знать по сути, тот факт, что все его верования верны. Так что, если все пропозиции Вр -> р истинен о вас, они могут не все поверят от вас. Вместо парадокса мы получаем результат неполноты. И вам действительно не нужно ехать на остров КК; Достаточно того, что некоторые жители утверждают: «Мистер Х или Мисс Х никогда не поверит, что я рыцарь». Это предложение будет верным, хотя X невероятно, независимо от того, встречал ли X такое предложение. Представьте себе туземную поговорку «бельгийцы никогда не поверят, что я рыцарь», тогда любой бельгиец, верящий в свою точность, т. Е. Верящий во все предложения Bp -> p, будет неточным, даже если бельгиец ничего не знал о Остров КК. Учитывая, что использование «верь» вместо «знай» устраняет парадокс, такой остров вполне может существовать, и утверждение его жителей может иметь последствия для нашей способности или неспособности поверить в какую-то правду! Это очень странная ситуация. Чтобы успокоиться, мы все еще можем надеяться, что такого острова не существует.

Но цель острова состояла в том, чтобы просто создать вымышленную ситуацию, легко иллюстрирующую, как кто-то может встретиться и поверить в какое-то само-ссылочное предложение. Это работает так: пусть k будет утверждением, что натив - это рыцарь, и предположим, что натив утверждает p. Тогда p будет истинно тогда и только тогда, когда k истинно, и если кто-то верит в правление острова (я помню: все рыцари говорят правду, все мошенники лгут, а все жители - мошенники или рыцари), он будет верить предложению (k <-> p).Теперь утверждение «ты никогда не поверишь, что я рыцарь», однажды утвержденное верующему в правилах острова, заставит самореференциальное суждение (k <-> -Bk) поверить этому верующему. Более того (k <-> - Bk) будет действительно верно в случае, если правила действительно действуют на острове.

Дело в том, что с островом К.К. или без него машины не могут так легко избавиться от самореференциальных утверждений. На самом деле машины не могут избавиться от них вообще. Есть известный результат, который доказывает этот факт, известный как лемма одиагонализации . Таким образом, с диагональной леммой мы можем рассуждать так, как если бы существовал остров КК, что делает неполным любое «проверяемое» убеждение третьего лица из честной универсальной машины. Читатель, который предоставляет это, может перейти к следующему более техническому разделу.

 

            Лемма о диагонализации .   Если у вас есть дублирующая машина D, которая при небольшом склеивании на любой машине M дублирует ее и вставляет немного, говоря, скажем, MM, то, если немного приклеить ее к самому DD, получится сам DD. То есть DD производит DD относительно некоторой вероятной универсальной вычислительной истории. В нашем болтливом подходе достаточно, чтобы машина верила элементарным отношениям замещения, таким как subst (abc, baX) = [baabc], что означает, что замена X во втором аргументе первым аргументом дает (описание) строку baabc. Скобка «[« и «]» используется для представления описания конечного результата в терминах объекта, о котором может рассуждать машина, например чисел нашей арифметической универсальной машины. Если машина помнит, что это всегда первый аргумент, заменяющий второй аргумент, она будет правильно полагать, что subst (aXc, baX) = [baaXc], хотя поначалу это может показаться немного запутанным из-за появления X в первой строке аргумента. Таким образом, машина поверит, и читателю предлагается проверить это руками, что:

                        subst (subst (X, X), subst (X, X)) = [subst (subst (X, X), subst (X, X))]

Мы получаем выражение, которое обозначает описание самого себя. Предположим теперь, что вы хотите построить машину, способную выполнять какое-то механическое преобразование на себе, применяя другую машину T к себе. Все, что вам нужно, это новая машина, которую я все еще пишу D, способная, если вы представите ей машину A в качестве входных данных, чтобы применить T к результату приклеивания немного A к себе раньше: DA дает T ([AA]). Тогда DD даст T ([DD]).   Применение этой идеи в нашей болтливой замене приводит к выражению, способному произвести трансформацию самого себя, и этому способ, в который машина может поверить. Давайте возьмем любое прилагательное, понятное для машины. Они называются предикатами в логике. Например, предикат odd (X), который говорит, что X нечетен;например, нечетное (23) является истинным предложением, а нечетное (24) является ложным. Нечетное (X) легко понять с помощью нашей арифметической машины: нечетное (X) <-> существует число Y такое, что X =      (2 раза Y) + 1.

            Определим 1) T (X) как нечетное ([subst (X, X)]) и 2) пусть m = [T (X)]. Машина будет полагать, что T (m) эквивалентно нечетному ([subst (m, m)]) и, следовательно, эквивалентно нечетному ([subst (m, [T (X)])]), 2, и, таким образом, эквивалентно нечетному ([subst (m, odd ([subst (X, X)])])), таким образом, эквивалентно нечетному ([odd [subst (m, m)]])), таким образом, эквивалентно нечетному ([T (m )]). То есть: машина будет считать, что предложение T (m) эквивалентно нечетному (T (m)). Определим замкнутую формулу с помощью T (m) как k: мы имеем, что машина верит в k <-> нечетно ([k]).

            Так что k верно, если его описание на машинном языке странно! Теперь, выбор предиката «нечетный (X)» не имел никакой релевантной роли в доказательстве, поскольку он определим в машинном языке, и мы проиллюстрировали, что для любого такого определяемого предиката P существует соответствующее предложение k с фиксированной запятой такое, что машина верит (k <-> P ([k])).

Теорема. Для любого предиката A, определяемого на машинном языке, существует такое предложение k, что машина будет знать (правильно верить) это предложение (k <-> A ([k])). Другими словами, с упрощенными обозначениями для любого определяемого предиката P логическое уравнение X <-> P (X) допускает решение k такое, что машина считает, что k <-> Pk.

 

Последствия леммы о диагонализации огромны. Дело в том, что машинам больше не нужно посещать остров КК, чтобы испытывать беспокойство из-за всевозможных ссылок на себя. Что происходит с парадоксами? Что если туземец просто говорит: «Я не рыцарь».Традиционный способ избежать парадокса состоит в том, чтобы сказать, что ни один местный житель никогда не скажет, что, если это не так, нас приведет к полному противоречию. Предположим теперь, что понятие рыцаря можно определить в машинном языке с помощью предиката knight (x), означающего, что x называет истинное предложение, так что машина верит для любого предложения p: p <-> knight (p). Тогда, применяя диагональную лемму к предикату, определенному как «не рыцарь (x)»,   существует такое ak, что машина будет считать, что k эквивалентно отрицанию knight (k), что само по себе эквивалентно -k, поэтому машина будет верить k <-> -k: противоречие. Теперь, согласнопредположению леммы о диагонализации , это означает, что «рыцарь (х)» или «мошенник (х)» просто не определим на языке машины. Правда на машине не может быть названа машиной. Это версия теоремы Тарского. По той же причине, парадокс, который мы имеем выше, когда мы встретили туземца, говорящего нам: «Вы не узнаете, что я рыцарь», с соответствующим предложением с фиксированной запятой k <-> -Ck, показывает, что согласованное машинное знание не может быть определено последовательная машина. Что можно сказать о убежденияхмашины и , в частности, о передаваемых убеждениями от третьего лица нашей платонической системы SRC? От посещения врыцарь плутостровмы получили теорему о неполноте. Таким образом, по лемме о диагонализации мы получаем соответствующую теорему о неполноте для машины.

Если теорема Гёделя о неполноте удивительна, она ничто по сравнению с теоремой Лёба. Сначала нам понадобится следующая теорема суммирования.   Можно показать, что убеждения универсальной машины Платонизма описываются следующими доказуемыми (и верными с само-ссылочной интерпретацией) утверждениями:

1) Если M верит p, то M верит Bp     (M нормально)

2) M считает, что Bp -> BBp    (M знает, что он нормальный, мы будем говорить, что M имеет тип 4) 

3) М считает, что B (p-> q) -> (Bp -> Bq) (М считает, что он регулярен, то есть знает, что следует за Modus Ponens или MoPo). Эта формула называется K (для Крипке).

Я скажу, что нормальная машина является рассудителем типа 4, когда проверяет 1, 2 и 3. Строка 1 говорит, что машина нормальная. Можно сказать, что Bp-> BBp верно для машины, учитывая, что мы интерпретируем Bp машиной, считает p. Это можно рассматривать как форму самосознания. Вторая строка говорит, что для всех предложений машина считает, что это нормально по отношению к ним, это дает еще большую самоосознанность: не только Bp-> BBp верно в отношении машины (по строке 1), но строка 2 заставляет ее верить на машине [26] .Строка 3 говорит, что машина не только платонистская, в смысле наличия набора убеждений, закрытых для правила modus ponens, но на самом деле знает (правильно полагает), что она закрыта для MoPo.

Упражнения по ревизии: Давайте скажем, что машина точная, правильная или звуковая, если Bp-> p верно для машины. Допустим, машина устойчива, если для нее верно BBp-> Bp. Может ли точная машина поверить, что она точна в отношении любого предложения? Может ли последовательная машина верить в свою стабильность? Вы можете попытаться показать, что для любой непротиворечивой нормальной и стабильной машины существует неразрешимое предложение, т. Е. Предложение p, такое, что машина не может верить ни p, ни –p.

Некоторые полезные определения: машина M1 справочно верна относительно машины M2, если каждое утверждение, доказанное M2, верно для M1 (мы предполагаем, что истинные предложения, в которых нет символа B, являются вакуумно референциально истинными, например, 1 + 1 = 2 правда обо всех). Машина самореференциально верна, если она референтна относительно себя. Очевидно: SRC подразумевает надежность, подразумевает стабильность. Машина M1 является относительно полной на M2, если M1 доказывает все предложения, которые верны для M2. Вы можете показать, что самореференциальная корректность влечет за собой самореференциальную неполноту.

 

            Арифметическое плацебо, уверенность в себе и скромность.   Как насчет туземца, который говорит мыслителю следующее гораздо более позитивное предложение: «Вы будете верить, что я рыцарь»? На KK-языке это вопрос, который Л. Хенкин задал М. Х. Лёбу, что приводит Лёба к поразительному удивительному обобщению теоремы Гёделя. На языке арифметической классической машины, что можно сказать о предложении k, говорящем о себе доказуемо ([k]). Очевидно, что это предложение может быть сказано мошенником (и быть ложным) или рыцарем (и быть правдой). Это вполне в отличии от гёделевских предложений изученных ранее, на тип р <-> -bp,   которые говорят о себе ,что они не доказуемы М, что делает их истинными о М и недоказуемы на М, когда М последовательны, и делают их неразрешимо по M, когда M также устойчиво. Но лемма о диагонализации может ударить более глубоко и более позитивно, чем мы могли ожидать на первый взгляд.

Давайте вернемся на остров KK. Ученик 4-го типа, который является обычным платонистом, зная, что он нормальный, развивает некоторую тревогу по поводу экзаменов в конце года. Учитель сказал ему не беспокоиться так сильно, и его беспокойство было вызвано нехваткой уверенности в себе. Он сказал студенту, что если он сможет просто поверить в успех, он добьется успеха. Это не было большой помощью, поскольку тот факт, что ученику действительно не хватает такой уверенности в себе, и поэтому, хотя он доверяет своему учителю, что, если он когда-либо сможет поверить в успех, он добьется успеха, на самом деле это не так. веря в успех и вполне может потерпеть неудачу.   Затем учитель предложил ему посетитьрыцарь плут островГоворят, что есть уроженец, который был одаренной жрицей, специализирующейся на искусстве воспитания уверенности в себе. Студент полностью доверяет своему учителю и верит в правила KK, и поэтому решает отправиться туда во время пасхальных каникул, незадолго до экзаменов. Студент встречает жрицу и объясняет ей, что его учитель был доверчив, поэтому, если бы он мог поверить, что, если он когда-либо сможет поверить в успех, успех произойдет, но добавляет, что он на самом деле не верил в успех. После некоторой церемонии жрица в конце концов говорит ему: «Если ты когда-нибудь поверишь, что я рыцарь, то у тебя все получится».

Теперь ученик впадает в отчаяние. Он думает, что у него нет больше доказательств того, что жрица была рыцарем, чем он верил в себя с самого начала. Подумав дважды, он получает большое облегчение. Почему?

            Давайте предложим, что студент будет успешным. Ученик доверяет своему учителю, так что он верит Bs -> s.   Теперь он верит в правление острова, поэтому он верит, что k <-> (Bk -> s), где k - это предложение, что жрица - рыцарь. Студент сделал следующее рассуждение: «Давайте предположим, что я поверю, что она рыцарь, тогда я поверю тому, что она сказала, то есть Bk -> s (будучи типом 4, он знает, что он регулярный). Но если я верю, что она рыцарь, я поверю, что я верю, что она рыцарь (будучи типом 4, он знает, что он нормальный), то есть я поверю Бк; поэтому, если я когда-нибудь поверю, что она рыцарь, я поверю и Бк, и Бк -> с, поэтому с помощью логики высказываний я поверю с, и, поскольку я доверяю своему учителю, это означает, что я добьюсь успеха. Но именно это и сказала жрица: если я верю, что она рыцарь, у меня все получится. Так она сказала мне правдивое утверждение! Таким образом , она является рыцарем «. Будучи нормальным, ученик теперь будет верить, что она рыцарь, и поэтому верит также тому, что она сказала, что, если он считает, что она рыцарь, он добьется успеха. Поэтому он поверит, что у него все получится, и тогда, если его учитель был прав, он добьется успеха!

Теперь, согласно лемме о диагонализации, нет необходимости в универсальной машине типа 4 для поездки на остров КК. Просто существует предложение k с фиксированной запятой, такое что k <-> (Bk -> s), для любого предложения s, и приведенные выше рассуждения дают доказательство теоремы Лёба : если машина типа 4 считает Bp -> p для некоторого предложения р, то машина верит р.

Вот простое «следствие»: вторая теорема Гёделя о неполноте: если машина типа 4 последовательна, то машина не может поверить, что она последовательна.

Доказательство: согласованность на машинном языке –Bf. Но это Bf -> f для ПК, поскольку читатель может проверить это с помощью двухстрочной таблицы истинности. По Лёбу, если машина когда-нибудь поверит в Bf -> f, она поверит в f, что противоречит предполагаемой последовательности.

А как насчет вопроса Хенкина?   Непосредственным следствием теоремы Лёба является то, что предложение «Я доказуемо М» верно и доказуемо М! Это следует из того, что предложение p <-> Bp влечет, в частности, Bp-> p.

Отметим, что теорема Лёба может быть сформулирована как B (Bp-> p) -> Bp. Эта формула называется формулой Лёба и называется L. Эта формула верна для M, но M тоже в это верит. Универсальная машина типа 4 может даже доказать то, что мы только что доказали, а именно:

B (k <-> (Bk -> p))    ->    B (Bp-> p) -> Bp

И формула Лёба снова следует за посещением острова КК или, что более серьезно, из леммы о диагонализации формулы BX-> p. Рохит Парих назвал машину Лёбяна скромной, а формула Лёба - действительно формула скромности. Причина в том, что машина будет верить в свою точность по отношению к p, то есть верить Bp-> p, только когда она действительно верит в p. В этом случае Bp очевидно из MoPo, учитывая, что (p -> (q-> p)) является тавтологией. Поэтому трудно представить, как быть более скромным.

Определение . Машина типа 4 является скромной, если она считает, что все предложения B (Bp -> p) -> Bp.   Можно показать, что скромность влечет за собой веру в свою собственную нормальность, и поэтому мы будем равнодушно называть нашу машину SRC, которая доказуемо скромна, скромной или лёбовской машиной [27] . Универсальная машина типа 4 не нуждается в посещении острова КК, чтобы стать скромной, по лемме о диагонализации.

            Теоремы Соловея о неполноте-полноте В 1976 году Соловей дал две подлинные и замечательные теоремы о полноте, касающиеся (бесконечных) дискурсов, которые мы можем иметь с помощью арифметической машины Платониста SRC или более общих машин Лобиана и сущности [28] . В его первой теореме говорится, что скромная логика правдоподобия высказываний, Соловей по имени G, то есть нормальная система с аксиомами K и L, полностью формализует доказуемую арифметическую логику высказываний доказуемости и согласованности арифметики Пеано, или ZF, фактически любой обычной доказуемости. Предикат в RE устанавливает расширение PA. Это делает формулу L действительно фундаментальной формулой психологии машины. Известно, что 4 можно получить из L в G.

            Вторая теорема еще более удивительна. Рассмотрим следующую теорию G *, в которой аксиомами являются все теоремы G плюс формула разумности Bp-> p. И который закрыт для MoPo. Обратите внимание, что мы не просим G * быть нормальным по той причине, что в этом случае из инстанцирования аксиомы Bf-> f нормальность приведет к B (Bf-> f), а затем Löbianity приведет к Bf, и учитывая, что мы уже получили Bf-> f, MoPo приведет к f, что делает G * несогласованным. Вторая теорема Соловая гласит, что G * полностью формализует истинную арифметическую пропозициональную логику доказуемости и согласованности.

Теперь можно показать, что и G, и G * разрешимы, что делает корону G * минус G решаемым множеством, закрытым для MoPo, невероятной правды. Принимая нашу наивную позицию, это делает их не заразными, а также. Например, мы знаем, что SRC является последовательным, стабильным и надежным, но не может этого знать, и это делает -Bf, BBp-> Bp и Bp-> p принадлежащими G * \ G.Фактически, поскольку G закрыта для правила необходимости, G * закрыта для правила «возможности»: если p доказуемо G *, то -B- p также доказуемо G *. Разрешимость G и G * влечет за собой [29] разрешимость всех логик, которые следуют.

            Вычислительность.   Это гипотеза компьютерных вычислений, которая предложила нам взять интервью у самореференциально правильной машины. Такая машина может постоянно быть не вычислительной. Из-за неполноты непротиворечивой машине непротиворечиво верит в свою собственную непоследовательность, и действительно, вторая теорема о неполноте просто говорит, что: -Bf -> - B-Bf. Мы могли бы взять интервью у непротиворечивой, но не относящейся к самому себе правильной машины, и на самом деле мы могли бы взять интервью у не вычислительных машин, которые полагают, что теряют свою последовательность из-за телепортации. Но, как мы оправдываем в начале, нас интересует дискурс машины SRC в кадре компа . Теоремы о самоссылке и Соловье действительно оправдывают, что атомные , в логическом смысле, суждения соответствуют арифметическим суждениям, и это делает неизбежным использование G и G *. Теперь, чтобы принять во внимание comp и UD Argument, который показывает, что физические суждения возникают из суммы состояний, доступных для DU, мы должны ограничить эти арифметические суждения теми, которые доказаны или сгенерированы Арифметическим Доветейлером, то есть предложениями Sigma1 [30]. как объяснено в 8- ^м шаге УДА. Наша интроспективная универсальная машина знает, что они универсальны в том смысле, что для любого предложения p сигма1 машина может доказать, что если p истинно, то p доказуемо: они могут доказать p-> Bp. Таким образом, чтобы ограничить дискурс SRC в кадре компа, и таким образом обогатить логику самоссылки, достаточно добавить в G предложение p-> Bp с p атомарным. Мне нравится называть 1 предложением «p-> Bp» с p-атомарным из-за его фундаментальной важности, но также как сокращение Sigma1. «1» можно рассматривать как аксиому компа, записанную в виде (схемы) формулы, добавленной к G, и, следовательно, принадлежащей (бесконечному) дискурсу SRC в кадре компа . В моей предыдущей работе я использовал только арифметическую правильность этой новой логики, но логик Альберт Виссер (19) действительно доказал правильность и полноту G + 1 и соответствующей ему теории (G + 1) * истинности. Виккерс также дает независимые мотивы для подобного понятия проверяемости, и я привык называть G + 1 и (G + 1) *, V и V * соответственно [31] . Обратите внимание, что буква предложения p в p-> Bp не может быть заменена какой-либо формулой, а только буквой предложения, если мы хотим сохранить правильную интерпретацию арифметического дискурса. В качестве контрпримера p-> Bp противоречило бы неполноте в случае замены p на –Bf.

Если вы отождествляете логику с ее набором теорем, у вас есть следующий ромб, который я буду называть базовым ромбом для дальнейшего использования. Неявные ребра представляют собой включение:

 

                                                               V *

                                                         G * V   

                                                               грамм

 

Поднимаясь в северо-ЗападНаправление - это нетривиальный геделевский переход от доказуемости (правдоподобности) к истине. Подниматься в северо-восточном направлении - нетривиальное направление. Иногда, чтобы исправить ситуацию, я говорю, что G дает науку, а G * дает теологию, V дает комп-науку, а V * дает компеологию. Но это можно взять с небольшим количеством соли [32] .

 

Арифметический Теэтет.   Мы еще не в состоянии получить физику. Чего не хватает, так это фундаментального различия между точками зрения от первого и третьего лица, без которого аргумент UD просто не начинается. Четыре G, G *, V, V * дают описания только от третьего лица. Например, G полностью аксиоматизирует пропозициональную логику самореференциально правильного дискурса, сделанного платонистскими машинами, но эти машины говорят о себе только через описание от третьего лица (построенное) на правильном уровне.Например, арифметическая доказуемость Пеано описывается в терминах чисел, часто называемых числами Геделя.

Но аргумент универсального доводчика (UDA) действительно показал, что физика должна проявляться с точки зрения машины от первого лица или с точки зрения множественного числа от первого лица. Эти точки зрения от первого лица касаются ожиданий последовательного расширения некоторых личных, вопросительных, возможно, бессознательных большую часть времени, но сознательных перед врачом, ставок на самосогласованность.

            Чтобы опросить Универсальную Машину, нам нужно определить те точки зрения, с которых машина может разговаривать. Мы будем следовать двум идеям и их объединению: 1) определить первого человека знающим, то есть того, кто правильно верит предложениям. Это один из хорошо известных (философов) Театетов пытается определить знание на основе мнения после того, как Сократ спросил его, в «Театете» Платона. 2) определить первое лицо (множественное число?) По лучшему. С первой идеей мы даем верующему нерушимую пуповину с истиной, делающую ее неисправимой, какой должен быть знающий. Со второй идеей мы присоединяем верующего к некоторой (надеюсь, правильной) ставке на его собственную последовательность. По крайней мере, формально, мы можем вообразить объединение этих двух идей для получения правильного лучшего . Все три идеи могут быть определены в логике самореференции:

 

            Чтобы узнать p, написанное Cp, определяется как   Bp & p,

            Ставка на p, написанная Pp, определяется как   Bp & -Bp,

            Чтобы правильно поставить на P, написано Op, определяется   Bp & -Bp & p.

 

Это имеет смысл: G * действительно доказывает, что Bp эквивалентно Cp, Pp и Op, но с точки зрения машины (Bp <-> Cp), т. Е. (Bp <-> Bp & p) ни правдоподобно, ни познаваемо, что доказуемо Г; также G * -эквивалентность (Bp <-> Pp) и (Bp <-> Op), (Pp <-> Op) доказуема G.   Это следует из простых фактов, что G *, в отличие от G, доказывает Bp   -> p, а G * доказывает p -> - Bp. Все арифметические реализации соответствующих модальных логик, где буквы предложения интерпретируются арифметическими предложениями, доказывают одни и те же арифметические предложения, но с машинной точки зрения они дают очень разные логики. Эти варианты определения Театета описывают различные способы, которыми машина может быть связана с истиной, и эти способы являются онтико-эквивалентными (по G *), но эпистемически-неэквивалентными (по G). И все эти замечания G / G * можно снять с помощью ограничений comp V / V *, где буквы предложений интерпретируются предложениями Sigma1. Таким образом, применяя три варианта Theaetetus к каждой логике, взятой из основного алмаза, мы получаем 12 логиок. На самом деле мы получаем 10 логик, потому что две из полученных логик могут быть показаны равными: G * и G дают одинаковое знание (Cp), а V * и V дают одинаковое «знание comp». Это означает, что с точки зрения знающего, правдоподобие приравнивается к истине. Это делает его сродни конструктивистскому саморасширяющемуся я. Как и в теории сознания Брауэра [33] , это «я» не может быть названо само по себе, и это следует из того факта, что Cp, как было показано, не может быть определен машиной. Таким образом, знающий не может поверить, что он является каким-либо другим устройством с именем от третьего лица, и это может объяснить некоторое нежелание первого человека делать ставку на искусственное цифровое тело или бояться цифрового дублирования.Применение вариантов CP на G ⁽ * ⁾ хорошо изучено в литературе. Это было сделано независимо от Булоса, Гольдблатта, Кузнецова и Муравицкого. Артемов делает диссертацию [34] . Это дает логику необратимого (антисимметричного) субъективного «времени», совершенно сходного в этом отношении с теорией сознания Брауэра. И это было подтверждено (не доказано!) Результатом самого Голдблатта (связанного с некоторыми работами Геделя, Маккинси и Тарского), связывающего S4Grz (читайте S4 Grzegorczyk, это результат варианта CP на G ⁽ * ⁾ ) и интуиционистская логика. Заметим, что философы, которые не принимают определение знания Cp-Theaetetus, неявно или явно делают вид, что способны отличить состояние бодрствования от состояния сновидения, и, таким образом, отрицают самую примитивную форму comp, как это было предложено шаг 6 в УДА. В качестве примера, философ-позитивист Малкольм пытается опровергнуть [35] существование сознания во сне и в машине. Он сравнивает осознанное сновидение «Я мечтаю» с ложным предложением Эпименида «Я лгу», G и G * делают возможным более точное сравнение. S4grz - это пропасть интересных вещей, которые можно сказать о психологии первого лица машины, но я отошлю читателя к моей «Совести и механизму» для получения дополнительной информации, потому что пора взглянуть на физику и ощущения.

 

            Физика и ощущения Чтобы получить физику и ощущения, мы должны применить варианты Theaetetus к V *. Это единственный способ найти «истинную» логику вероятностной меры на всех непротиворечивых расширениях (это объясняет звезду *), возникающую, когда атомные суждения ограничены теми, которые доступны универсальному голубятнику (сигма1, это объясняет V = G + 1).

            Чтобы получить модальную логику с понятием вероятности, и теория моделей, и модальная семантика, которые немного выходят за рамки данной статьи, предполагают необходимость наличия деонтической формулы Np -> -Np, где N - абстрактная модальность необходимости. во-первых. Идея состоит в том, что Np означает P (p) = 1, причем P (p) интерпретируется как вероятность p, а затем -P (-p) означает   «P (-p) отличается от 1», что означает «P ( p) отличается от 0 ”, что делает деонтическую формулу естественной для понятия вероятности. Заметим, что ни G, ни G * не доказывают это (G * не доказывает Bf -> - Bf, в действительности G * доказывает Bf-> Bf). Теперь все логики, полученные с помощью вариантов Theaetetus, дают логику, проверяющую деонтическую вероятностную формулу. Естественно, Pp-вариант является буквальным переводом следствия UDA, поэтому он должен, с учетом гипотезы, дать физическую вероятность. Таким образом, вариант Pp, который дает модальную логику с «вероятностью один» или «мерой один» в последовательных расширениях, должен давать логику меры один в физических предложениях. Поэтому нам нужно посмотреть, что говорит физик о такой логике, и посмотреть, что говорит вариант Pp на V *, а затем сравнить.

            Вначале я сказал, что Квантовая физика является хорошим кандидатом на то, чтобы стать стабильной частью фундаментальной физики. Теперь квантовая физика по сути является исчислением вероятностей. Фон Нейман разработал, с помощью биркгофовых, логики квантовой вероятности один . В квантовой физике миры или состояния представлены линией в гильбертовом пространстве. Предложения представлены линейным подпространством. Подобно тому, как булеву классическую логику можно интерпретировать как решетку подмножеств множества, так же как и брауверскую интуиционистскую логику можно интерпретировать как решетку открытых множеств топологического пространства, квантовую логику можно интерпретировать как решетку подпространств гильбертова линейное пространство.Каждое «под-понятие», с модальной точки зрения, можно рассматривать как и суждение, и как «совокупность» миров, в которых это суждение истинно. Модульность решетки (ослабление булевой дистрибутивности) дает надежду фон Нейману захватить полную логику ортогональных экспериментов типа да-нет, способных дать все квантовые вероятности. Увы, бесконечное измерение убивает модульность, и фон Нейман перепрыгнет из гильбертова пространства в алгебры… фон Неймана. Тем не менее, он останется неудовлетворенным квантовой логикой, которую он выделит [36] , и, как писал ван Фраассен, физики сталкиваются с лабиринтом квантовой логики.

            Так что, если честно, я пока не знаю, хорошие это или плохие новости, для тех, кто хочет, чтобы комп был подтвержден или опровергнут, но не только Pp, но также Op и даже Cp, когда они применяются на V * приводит к причудливым и разным видам арифметической квантовой логики. Как?

            Определение Модальная квазиквантовая логика имеет в качестве основной аксиомы p-> BMp (p атомарный). Мне нравится называть эту формулу «LASE» для «Маленького абстрактного уравнения Шредингера». М является аббревиатурой от -B-. Модальная квазиквантовая логика также имеет аксиому Bp -> p (T) с K   B (p-> q) -> (Bp-> Bq) и является замкнутой для MoPo, но необязательно для правила вывода необходимости ( = не обязательно нормально).

Почему? Гольдблатт показал, что логика B, известная как система Брауэра, и которая является модальной логикой с K, B (p-> q) -> (Bp-> Bq)  и LASE, p-> BMp и T, Bp-> p, и это нормально, аксиоматизирует квантовую логику (в классическом сеттинге), аналогично аксиоматизированной интуиционистской логике S4Grz (в классическом сеттинге).

Точно, учитывая следующее преобразование GOLDB, благодаря Голдблатту 1974, из языка высказываний в модальный язык высказываний, который преобразует буквы предложения p в BMp и преобразует -p в Bp, а также рекурсивно (A & B) в (GOLDB A & GOLDB B), Голдблатт показал [37], что формула A доказана в минимальном варианте квантовой логики, если B доказывает GOLDB (A).

Теперь модальная квазиквантовая логика, благодаря правде LASE для атомарных предложений, обладает всем, что необходимо для применения преобразования Гольдблатта для получения разумной арифметической квантовой логики. Применение вариантов Cp, Pp и Op Theaetetus к алмазу базовой логики дает, как мы ожидали от UDA, по крайней мере с вариантами Pp, три модальные квазиквантовые логики. Это те, которые называются S4Grz1, Z1 *, X1 * соответственно, в моей докторской диссертации «Calculabilite, Physique et Cognition [38] ».

 

                                      S4Grz ¹                      Z1 *                      X1 *

                               S4Grz    S4Grz ¹           Z *        Z1             X *      X1

                                      S4Grz                         Z X                          

 

Применение (обратного) преобразования Голдблатта к S4Grz1, Z1 *, X1 * дает три арифметические квантовые логики AQL ₀ , AQL ₁ , AQL _{2, которые}  приводят ко многим открытым проблемам. Есть ли у нас модульность, или ортомодулярность, или что-то еще? Являются ликолоколНеравенство нарушено

 

Я предполагаю, что квантовый компьютер может быть определен в AQL _i или в их расширениях первого порядка (с квантификаторами).Это объясняет, почему любая универсальная машина, смотрящая на себя, обнаруживает квантовую «реальность» как меру своих наиболее вероятных правильных ожиданий.

 

Применяя преобразование Голдблатта к непустому набору пропозиций Z1 * минус Z1 и X1 * минус X1, это дает описание непротиворечивой (и истинной) физически измеримой, но неинфекционной истины, так что «квалиа» или ощущения , сами описываются видами квантовой логики [39] . Это главное преимущество компа по сравнению с традиционной эмпирической физикой. Эмпирическая физика, очевидно, заранее по сравнению с физикой компов, но по методологии почти обязана поставить первого человека под ковер, и поэтому скучает по Qualia Logics.

Комп делает их возможными и необходимыми, и изолирует их от многих модальных нюансов, навязанных неполнотой Лёбова.

                                                                                                  Брюссель, 14 августа 2004 г.

 

---