Систематизация и связи

Философия науки и техники

Евклидова геометрия - базис элементарной геометрии - построена на пяти аксиомах (элементах). 

 

1. "От всякой точки до всякой точки можно провести прямую линию.
2. Ограниченную прямую можно непрерывно продолжать по прямой.
3. Из всякого центра всяким радиусом может быть описан круг.
4. Все прямые углы равны между собой.
5. Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых углов, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых углов."

 

В физической картине мира эти принципы приняли форму "однородности и изотропности пространства", оспоренные Эйнштейном. Согласно его теории пространство-время представляет собой единое целое и сами геодезические линии - искажены массой. Если бы тела не имели массы - движения небесных тел - строго подчинялись бы элементарной геометрии. А это, согласно точным наблюдениям, не так. 

 

Здесь - в теории Эйнштейна - есть парадокс. Следы мухляжа с математикой. Что же именно искривляет пространство-время? Масса или предельность скорости света? По сути, Эйнштейн создал две разные теории относительности, специальную и общую. По одной теории - пространство-время искривляет предельность скорости света, а по другой - масса. 

 

Теория Эйнштейна построена на тензорном математическом аппарате - развитии неевклидовой геометрии, но применение выводов математики в физике - всегда неоднозначно. Требуется талант физика, разглядеть связь математики и природного процесса. Правильно обозначить одно другим. Найти и решить концепт противоречащих точек зрения. 

 

Именно однозначность была троянским конём евклидовой геометрии в неевклидовой. Приняв новые принципы, приняли и устаревший принцип однозначности. 

 

Математика Евклида была уличена в неточности ещё эзотериком Пифагором, а именно - частный случай соотношения сторон треугольников был принят общим. Что определено (в общем виде, не именно для теоремы Евклида -.Аристотелем) одной из форм софизма, выдача частного за общее. Но, если нас устраивает лишь качественная, приблизительная оценка - этим искажением результата можно пренебречь. 

 

Платон вообще заявил, что "ни один текст не серьезен, особенно письменный и особенно, если он действительно о чем-то важном для его автора, ведь пишет и читает его не Бог, но человек". Что не помещало ему, в том-же тексте изложить пересказ даосской теории сочетания стихий... Пусть и упрощённо (схематично). Описывая дискурсивное мышление, как пример человеческой глупости. 

 

Аристотель сказал практически то-же самое: "Единственный собеседник человека, высказывания которого внутренне (естественно) достоверны - Бог", как персонофикация "сферы неподвижных звёзд, сотканных из эфира достоверности высказываний". "А человек, высказывания которого внутренне не достоверны и сам не понимает что говорит", "но, если продолжает говорить, то это пустая риторика - софизм". Попытка подчинить более слабое мышление - более сильному. 

 

Зачем? 

 

По неведению (глупости) или для перераспределения социальных благ. 

 

Насколько мне известно, первым исследовал принцип неоднозначности - Аристотель. Он рассмотрел две очерёдности трёх качеств представлений его современников о своих высказываниях:

 

1) Категоричность, тип высказывания и посылка.

 

2) Тип высказывания, категоричность и посылка. 

 

Первое (это уже переинтерпретация аристотелевской аналитики Чарльзом Пирсом, в конце 19-го века) - характерно для речи интеллектуала, придающей внутренней оценки достоверности сказанного форму и интерпретирующей такую форму смыслом, второе - обывателя, оценивающего достоверность формы посетившей его идеи и интерпретирующей её смыслом. 

 

Это два модуса речи: 312 и 132. Условно 3/2 и 1/2. 

 

При, казалось бы, одинаковых значениях типа высказывания (формы идеи), посылки (смысла) и категоричности (дефиниции) - интеллектуал и обыватель не поймут друг друга. Точнее - каждый поймёт что-то своё. 

 

Платон объяснял такое непонимание людьми друг друга иначе: "человек, мыслящий четырьмя стадиями речи (то есть дискурсивно, сочетая 1-имена чувств идеи, 2-точное определения словом (концепции, теоремы), 3-рисунки (метафоры, иллюстрации или доказательства) и 4 - понимание, в любой комбинации, но у даосов таких стихий мышления - 8, это и есть квантовый регистр - три бит) - никогда не поймёт человека, мыслящего пятью стадиями речи (пятая - непосредственное ощущение идей, созерцание). 

 

Конфуций считал одним краем пропасти непонимания людьми друг друга - желание поделиться с другими своим духовным открытием (созерцанием идей), а другим - обычай, как нежелание выслушивать подобные откровения других людей. 

 

Мост над этой пропастью - творчество - прагматический дицент, абеляровский концепт, консенсус всех дискурсов (он-же - общечеловеческая солидарность вне зависимости от точек зрения на истину) - Ричарда Рорти, бахтинский принцип единства означающего (смыслоформы идеи, житейской обыденности) и означаемого (самой идеи, искусства). 

 

У Конфуция - это гармония стихий по правилу двойного золотого сечения - пересечение двух из пяти лучей пентаграммы стихий, но пентаграмм - две, один из лучей у них общий, поэтому базовых стихий природы не пять, но 8.)

 

Терминологией Чарльза Пирса - семиотические знаки речи будут отличаться модусом. Пирс рассмотрел такие модусы речи в более общем случае реплик семиотического знака. Что совсем не тоже самое. Реплики - вариации значений трёх аспектов знака. 

 

Математический объект множества семиотических знаков (шести бит - 000000) - специальная унитарная группа Софуса Ли. 

 

Необходимо пояснение: согласно теориям и Аристотеля и Пирса, высказывание человека (у Аристотеля корректней - общепринятое - в ту или иную эпоху - представление человека о структуре своего высказывания) - как-бы (но никто не утверждал, что это именно так) - представляет собой трехмерное евклидово пространство. Если пространство - то с оговорками, что это негеометрическая (неевклидова) матрица. 

 

Какая именно? 

 

SU(3). 

 

Три аспекта знака - это три оси координат: 

 

1) Высота условного куба пространства мышления - тип высказывания (форма идеи): 

 

- низ - отрицающее (отрицающее символическую форму идеи, то есть - буквальная, реалистическая, иконическая форма), 

 

- верх - утвердительное (утверждающая символ - символическая форма - мудрость), 

 

- середина между ними - неопределённое (строго говоря - это уже терминология Пьера Абеляра из 12-го века - либо концепт, непротиворечивое единство иконы и символа, то есть - и то и другое, либо-же - не то и не другое). Сейчас мы скажем - это два спина среднего значения аспекта знака речи - либо концепт, либо его симулякр). 

 

Аристотель не отрицал спин, но и не сформулировал его теорию, не дал ему чёткого определения. У него есть неоднозначный средний элемент и все. У Пирса - только концепт, симулякр не рассмотрен, видимо потому что - зачем рассматривать обман? 

 

2) Длина - посылка или смысл:

 

- передняя грань куба мышления - частное (терминологией Канта - максима, частный интерес),

 

- задняя грань - общее (у Канта императив - власть Закона, важное для всех людей),

 

- среднее - неопределённая посылка (сейчас мы скажем факт (лицо факта - в теории постживописной абстракции Клемента Гринберга) или поддельный факт. 

 

В семиотике, смысл - это интерпретация человеком формы посетившей его идеи. Пирс критиковал терминологию Канта, за возможность искажения (подделки симулякрами), но его собственный вариант терминов - трудновыговариваем, поэтому прижились кантовские определения смысла. С поправкой на два возможные спина. 

 

Термин спин заимствован в физике элементарных частиц. Там он был обнаружен экспериментально, как 1/2 (адроны, кварки, лептоны) и 3/2 (гепироны). Но, внятно никак не объяснён. "Структурное свойство бесструктурной (элементарной) частицы" - звучит не убедительно. Если есть структура, то частица не элементарна, если частица элементарна, то у неё нет никакой структуры. Решение противоречия - неоднозначность (спин). 

 

Без учёта спина - материя барионна, но помимо такой барионной материи обнаружены (разумеется - косвенно, это абстракции, как и сами частицы барионной материи) - переносчики взаимодействия между такими "элементарными" частицами - бозоны (это фотон, глюон - но,  я не согласен с определением глюона бозоном, у него иная геометрическая природа (глюоны - альтернатива кваркам: либо мы считаем, что частицы состоят из кварков, либо из глюонов - и это - две равноценные точки зрения), Зет, Дабл-Ю бозоны, их спин - единица и Аш (бозон Хиггса, только у него нулевой спин). Спин бизонов - ноль или единица. Хотя... Вероятно это уже не спин, но какое-то иное качество неоднозначности. Терминология явно запутана. 

 

3) Ширина куба - категоричность (в семиотике Пирса - самооценка человеком достоверности означение идеи её смыслоформой, сейчас мы скажем - дефиниция:

 

- левая грань куба - возможное (возможно присуще, гипотеза, самоирония относительно единства означающего и означаемого ),

 

- правая - именно присуще (аргумент единства означающего и означаемого ),

 

- среднее - либо само единство означающего и означаемого (художественный образ, равный результату научного эксперимента, дицент, консенсус, силлогизм как единство вопроса и ответа. вопроса как указание на противоречия в словах собеседника и ответа, как аргумента отсутствия такого противоречия), либо его симулякр (культура, обычай, тот или иной дискурс - сословная правда, корпоративный интерес). 

 

К чем это все?

 

Представляя пространство мышления геометрически - например кубом (евклидово пространство) - мы теряем спины средних значений. 

 

У евклидового куба только 8 вершин (так и есть, их спин один, это квантовый регистр), 12 рёбер (с учётом спина - 24), шесть граней (с учётом спинов - 24) и одно внутреннее пространство (с учётом спинов - 8). 

 

В евклидовом кубе - 27 элементов, в объекте с учётом спина - 64. Такой объект есть пересечение или сочетание двух квантовых регистров.  

 

Что есть геометрический объект с 8 вершинами, 24 рёбрами, 24 гранями и 8 внутренними пространствами? 

 

Это множество сочетаний элементов двух квантовых регистров. Но, сочетающихся регистров может быть сколько угодно и сложность объекта, от числа сочетающихся регистров - возрастает. 

 

В какой-то степени приближения - с оговорками - этот объект напоминает четырёх-мерный гиперкуб, но и такая геометрическая метафора будет не точна. 

 

Когда сочетаются два таких негеометрических (неевклидовых) объекта - картина ещё более усложняется. А число сочетаний квантовых регистров - неограниченно. 

 

Это цепочки знаков, не имеющие точной евклидовой геометрической формы, но точно записываемые двоичным кодом. Иероглиф-матрица - все более детально описываемого квантового регистра, где бесконечно подробное текстовое описание соответствует бесконечному числу оговорок относительно евклидовой геометрии объекта. 

 

Представить все эти произвольные сочетания нулей и единиц - сложно, поэтому на помощь и приходит то или иное упрощение - геометрия. А сама математика - лишь множество сочетаний своих постулатов. Измените постулат - изменится и сама математика - искусственная матрица применения своих базовых принципов. 

 

Постулаты - это общепринятые в ту или иную эпоху представления человека. Их можно проанализировать, как сделал Аристотель. Прийти к матрице представлений того или иного исторического времени. Но, это не матрица законов природы, а лишь матрица человеческих представлений о природе, общепринятых - в ту или иную эпоху. Не стоит этого забывать. 

 

Математик (геометрий) можно быть сколько угодно, но общепринятой ту или иную матрицу делает её социальная польза. Так, что это, как не социальная матрица, лишь выдаваемая за абстрактную (математика), риторическую (гуманитарное знание) или природную (физика)?

 

Хотя, сама эта матрица куда интересней природы... 

 

Ведь, кроме неё - в плане познания - у нас ничего нет и именно она обманывает нас, заставляя думать, что мы познаём не матрицу своего мышления, но природу... Почему? Это её свойство. 

 

И конечно, всегда есть искушение применить математические теории для описания природы. Если это преследует социальную цель - утвердится в сообществе - задурить головы читателям - это социально оправдано. Но, если цель - подлинное познание природы, то это познание достоверно только после познания искажения познания природы матрицей познания. 

 

Определить и компенсировать такое искажение понимания - возможно, но только при осознанном отказе от преследования социальной выгоды от статуса знателя. Что - простому человеку - невозможно отделить от подлога... 

 

А вот и нет, по теории матрицы - возможно. 

 

Но, не только механика массивных тел, для космических масштабов, но и элементарная векторная геометрия, построенная на евклидовых началах - оказалась не точна. Известная с начальной школы теорема Пифагора, на самом деле, это теорема Евклида, графически опровергнутая (исторически - доказанная) Пифагором. 

 

Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов. Пользуясь методом Пифагора - нарисуйте эти квадраты гипотенузы и катетов буквально - квадратами - и сравните их площади - это несложно сделать с помощью ножниц - и вам будет очевидно, что теорема справедлива не для всех прямоугольных треугольников, а только для тех, у которых соотношение сторон - 3, 4. 5. Что знали ещё в древнем Вавилоне. 

 

3^2+4^2=9+16=25=5^2

 

Для всех остальных соотношений сторон прямоугольных треугольников - равенство будет выполняться лишь приблизительно. На это можно закрыть глаза только, если нас устраивает точность плюс-минус несколько процентов. 

 

Если речь идёт о деревьях Пифагора - это множество квадратов (фрактальное дерево), составленных в треугольники, то математический образ (определяемых теоремой Евклида) соотношений сторон приведёт к значительной ошибке. Если деревья Пифагора рассмотреть геометрической моделью разветвления природных процессов - как ветвей дерева, то описание этого процесса теоремой Евклида будет ошибочным, условная алгебра будет отличаться от практической геометрии. 

 

Пифагор - как раз - опроверг строгость теоремы Евклида и ирония в том, что авторитету его имени - как раз - и была приписана "точность" этой теоремы. Это простой пример искажения знания культурой. Пример симулякра концепта. 

 

Альтернативные элементарные геометрии. 

 

Аксиоматика Александрова, ректора ленинградского государственного университета в 1952-1964 годах. Золотого времени науки, ушедшего навсегда. 

 

Наша советская (ленинградская научная) геометрия. Не путать с московским (феодально-купеческим) её симулякром. 

 

Как на закате этого постмодернистского времени сказал Че Гевара "мы не можем знать, зачем нам жить, пока не будем готовы отдать за это свою жизнь". Социальный комфорт искажает любое знание, провоцирует превращение его в симулякр. Возможно, причина феномена ленинградского университета - блокада. Социальность (дискурс университета 4231) отступила перед дискурсом подлинного знания - 1324, инверсией университета. Кто знает? Но, феномен был, та-же теория Фридмана о смысле эйнштейновского лямбда члена... 

 

:-)

 

Кратко:

 

Определим термины: 

 

Точка - условно обозначается заглавной буквой - либо служит концом отрезка (условно обозначаемого прописной буквой), либо - лежит на отрезке (находится внутри отрезка, то есть - принадлежит к множеству точек отрезка). 

 

Очевидно, что здесь смешиваются понятия отрезка и множества точек: Один отрезок принадлежит другому, если множество точек первого - являются множеством точек второго. Один отрезок объединяется с другим, если объединяются множества их точек. Один отрезок может быть отложен относительно другого. Считаю это понятным, не требующим пояснения. Один отрезок пересекается с другим, если у них есть одна общая точка. Если существует хотя-бы один отрезок, то у него есть только два конца и его точки находятся на этих концах и между ними. Любые две точки можно соединить отрезком и только одним. 

 

/- Вот здесь я - но только - применительно к условно представляемому пространству внутри квантового регистра - не согласен. 

 

Подчеркну. Мои возражения - только относительно представления квантового регистра геометрической фигурой - кубом. Не рассматривая геометрически (евклидово) - пересечения множеств элементов квантовых регистров - такой проблемы нет. 

 

Но, если не рассматривать квантовый регистр, то тогда что рассматривать? Бездумную абстракцию? А зачем? Ради самого процесса? Это не продлится долго, очень скоро возникнут симулякры такого знания, более успешные социально...

 

Существуют восемь элементов квантового регистра (восемь возможных вариантов сочетаний значений трёх бит: 000, 001, 010, 011, 100, 101, 111).

 

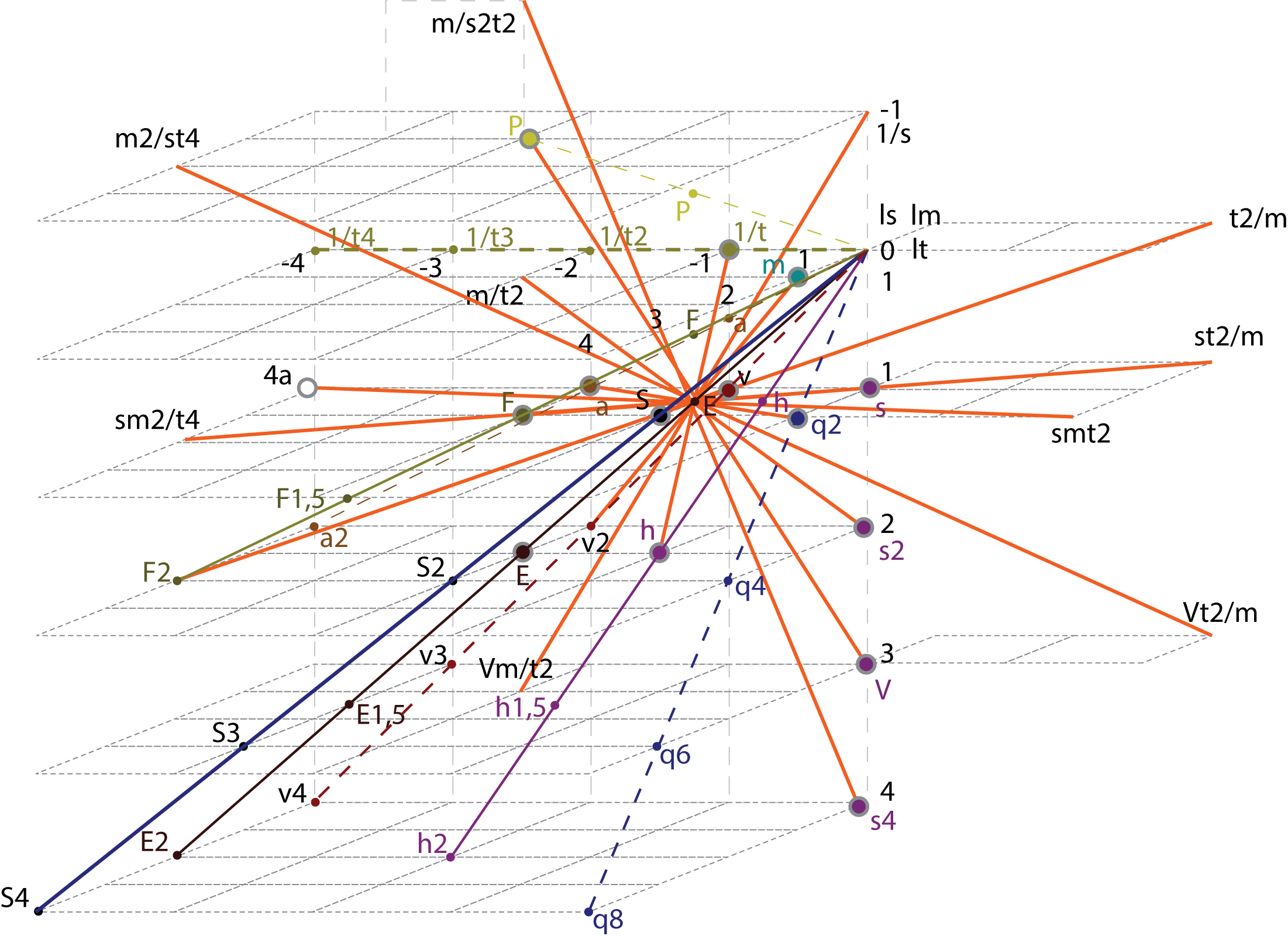
Если рассматривать "условное геометрическое представление (евклидово пространство) сочетаний элементов двух квантовых регистров", 8 х 8 = 64 варианта, то условные оси координат такого куба принимают вид: 

 

1/t - 1 - t 

 

(1/t=221=000110=110000=010100=100010 - четыре варианта - спина;

 

t=223=111001=001111=011101=101011 - четыре спина;

 

1=t/t - 4 x 4 = 16 вариантов: 

 

000110111001, 000110001111, 000110011101, 000110101011 (32131, 3234, 322311 - число чередующихся нулей и единиц),

 

110000111001, 110000001111, 110000011101, 110000101011 (-24321, -264, -25311, -241112),

 

01010011101, 01010000111, 0101011101, 010100101011 (11112311, 111143, 11111311, 1111211112),

 

100010111001, 100010001111, 100010011101, 100010101011 (-1311321, -13134, -1312311, -131111112). 

 

То-же самое - и для двух других осей. 

 

1/m - 1 - m

 

(1/m=322=100111, 111100, 110101, 101110,

 

m=122=000110, 110000, 010001, 001010),

 

1/s - 1 - s

 

(1/s=232=010111, 111010, 110011, 011110),

 

s=212=000101, 101000, 100001, 001100). 

 

Элементы квантового регистра, выраженные через эти пределы - физически - представимы так:

 

000 - sm/t - импульс или энтропия, что физически - одно и то-же: PV/T=E/T=S=mc2/c=mc=ms/t=p. 

 

001 - smt - куб единого заряда, усреднение времени, массы и расстояния. Либо же - произведение квадрата электрического заряда (q2=sm) и времени. 

 

010 - m/st - измерение условного "стандарта реальности" -  временем или произведение условного стандарта реальности и частоты.

 

011 - mt/s - произведение условного стандарта реальности и времени. 

 

100 - s/mt - измерение скорости массой, удельная скорость на единицу массы или произведение скорости и частоты. 

 

101 - st/m - отношение времени и условного стандарта реальности стандартной модели (в системе СИ "стандарт реальности" - m/s=m2/q2 - обратный квадрат электрического заряда - 1/q2, дело в том, что "условный стандарт реальности" - определён стандартной моделью базовых субатомных частиц, у которой своя система единиц, реальны или наблюдаемы только те частицы, стандарт реальности которых - определённая константа, все другие значения - человеком ненаблюдаемы, что не означает, что они в природе не существуют, стандарт реальности - фильтр человеческого восприятия природы. Возможно, есть и другие (нечеловеческие) восприятия, доступные нам лишь умозрительно, как абстракции. Но, доступные же. 

 

110 - 1/smt - обратный куб единого заряда. 

 

111 - t/sm - антиэнтропия. 

 

Но, если мы попробуем сочетать два элемента квантового регистра, то получим не исходный предел, а его квадрат:

 

000110=221=sm/t x 1/smt = 1/t2

 

Сочетая элементы квантового регистра, мы получаем квадраты пределов, а сочетая квадратные корни пределов - как это сделал Макс Планк в конце 19-го века - мы получаем элементы квантового регистра. 

 

Сочетая квадраты пределов, мы получаем квадраты элементов квантового регистра, а сочетая квадраты элементов квантового регистра, мы получаем четвёртые степени пределов. И так далее... Метафора капусты, множество логарифмических слоёв матрицы. И неопределенность - между этими слоями.  

 

Вопрос здесь лишь в том, уместно ли рассматривать условную геометрию информации? 

 

Если мы точно знаем, что такое представление неточно - по определению?

 

Где пример такого пространства?

 

Матрица физических величин. 

 

Матрица мышления человека, матрица языка, социальная матрица, матрица субатомных частиц и так-далее...

 

Не увидев - ту или иную - концепцию (точное словесное определение имён наших чувств невыразимой - трансцендентальной - идеи), нарисованной (геометрически) - нам её не понять. 

 

Геометрическое представление - как раз - и подводит нас к пониманию. Но, далеко не всегда, это частный случай - дискурс 43, точнее - 4321, дискурс риторики, один из множества возможных дискурсов, если частое представление названо общим - оно не точно, то и понимание ошибочно. 

 

А если познаваемый объект - жизнь, природа - принципиально не представим строго геометрически, то он и непознаваем. Если только мы не изменим правило своего понимания природы понимания. Не избавимся от диктата точной евклидовой геометрии. Рассмотрим её многовариантной, вероятностной. Примем за основу консенсус всех возможных дискурсов. 

 

Что есть такой консенсус всех возможных точек зрения? 

 

Образ Бытия Парменида. 

 

Если же игнорировать - очевидную - информационную структуру природы (как и мышления человека о природе), и рассматривать одно только воображаемое (геометрически идеальное) пространство, то там все - просто и понятно, но имеет лишь приблизительное отношения к природе и наоборот.

 

Я не согласен не именно с этой аксиомой элементарной геометрии Александрова, а с возможностью любой геометрии описать жизнь точно. 

Но, Гедель все это сформулировал ещё в 1931 году. Моя интерпретация его теоремы о неполноте: Строгая (однозначная, без учёта вероятности - спина) - формальная логика аксиом - сама по себе, а жизнь - сама по себе. 

 

Физика разных эпох различается математическим аппаратом. 

 

Это очевидно, теория дифференциалов (производных) и интегралов (перевообразных) классической механики (включая термо и электродинамику) - отличается от тензорной теории относительности - именно евклидовым и неевклидовым геометрическим представлением природных процессов. Сами процессы одни и те-же, но описанные по разному. 

 

Как и - основанная на матрице специальной унитарной группы - квантовая хромодинамика. Различный математический аппарат приводит к различному описанию одного и того-же. Поэтому и возможна универсальная модель - теория теорий - матрица представлений, частными случаями которой являются сами - все эти различные идеологии или мировоззрения. 

 

Простой пример. 

 

Конъюнкция (логическое И) и дизъюнкция (логическое ИЛИ), как и обратные им операции (не-И, не-ИЛИ), при определённом взгляде на множество решений уровненная с двумя двоичными переменными и одним решением - представляют собой множества из четырёх (из восьми) элементов квантового регистра. Спинов у каждого оператора - четыре. Но, сочетая (пересекая) два логических оператора - мы находим два общих элемента), тем самым - снижаем спин (многозначность) до двух. А разнося эти варианты по противоположным углам условного геометрического представления квантового регистра - куба квантового регистра, добиваемся однозначности. 

 

Конец моего замечания. -/

 

Любая точка отрезка делит его на две части и является единственной их общей точкой. 

 

И наоборот, два отрезка имеющие общую точку (опять - моё замечание - могут быть, а могут и не быть) частями одного отрезка. (Если они не расположены на одной прямой, то нет, но прямая то - как раз - и не определена, без принятия пяти аксиом Евклида, теория Александрова не имеет достаточного основания, а приняв аксиоматику Евклида, зачем нам другая?).  

 

Для любых двух (моё замечание - параллельных, но параллельность тоже не неопределённа) отрезков существует только один третий, равный одному и налегающий на другой. 

 

Два отрезка, каждый из которых равен третьему - равны. 

 

Далее:

 

Два отрезка, равные одному и тому же отрезку, равны друг другу. Если С на АВ, С' на A'B' и АС = А'С' и ВС = В'С' то AB = A'B'."

 

Далее у Александрова следует так называемая "аксиома Архимеда" - отрезок может быть разделён на меньшие - равные по величине (но сама такая величина - чётко не определена) - отрезки. (Тогда сам отрезок можно представить произведением такого "дифференциального отрезка" и его числа.) Если существует бесконечная последовательность вложенных друг в друга отрезков, то у всех них существует общая точка. 

 

 

 

"Точки CD лежат с одной стороны от а, если отрезок CD не пересекает никакого отрезка, содержащего а.

Точки А, В лежат с разных сторон от а, если напротив, отрезок АВ пересекает какой-либо отрезок, содержащий а."

"По отношению к каждому данному отрезку а все точки, не лежащие ни на каком отрезке, содержащем а, делятся на два класса — в один класс входят точки, лежащие с одной стороны от а, а в другой точки, лежащие с другой стороны от а, причем в каждом классе есть точки."

Угол - пара отрезков с одним общим концом - точкой. 

Если эти отрезки - стороны угла - общая точка его вершина. Далее даётся определение настоящему углу, а значит и подразумевается и ненастоящий, что опущу для краткости. Поперечина угла - отрезок между другими (по отношению к вершине) концами угла. Угол (два отрезка с отец вершиной) и его поперечина образуют треугольник (я бы назвал этого геометрический объект "замкнутым углом", а угол - "незамкнутым треугольником"...). 

"Два угла называются смежными, если у них одна сторона общая, а другие образуют вместе один отрезок не налегая друг на друга. Угол равный своему смежному, называется прямым. Если отрезки AC, BD равны и идут в одну сторону от отрезка АВ под прямым углом, то CD = АВ."

В целом, аксиоматика Александрова - конечно - на любителя. Я привёл её лишь в качестве примера непротиворечивой альтернативы евклидовой аксиоматике. Существуют и другие альтернативы. 

Здесь - важно увидеть сходство геометрии Александрова с формальной логикой Теофраста, отличной от Аналитики Аристотеля. 

В формальной логике рассматривается уже не пространство перересечения двух квантовых регистров (при скоромном аристотелевском умалчивании определения спина), как в интерпретируемом оригинале Аристотеля, но лишь правая (предельно категоричная) грань такого пространства. 

В формальной логике - всего 4 логических элемента (термины - A, E, I, O), вместо 27 аристотелевских терминов - позже названных семиотическими знаками (которых, с учётом спина, который был известен даосам - задолго до Аристотеля - 64). 

То есть, формальная логика - является радикальным упрощением матрицы даосских состояний природы - в 16 раз, а аристотелевской аналитики - в 6,75 раз. Если проводить сравнение по числу терминов (элементов матрицы). Что же это, как не подмена теории объекта (общепринятых - в античную эпоху - представлений человека о структуре своего высказывания - поверхностными признаками? То есть - софизм. 

Второе отличие - формальная логика рассматривает 4 варианта только одной из трёх аристотелевских фигур (вариантов суперпозиции терминов). 

1>2>3

1>2<3

1<2>3

1<2<3. 

Аристотель рассмотрел три другие фигуры (суперпозиции трёх терминов - за подробностями отправляю читателя к Аристотелю) и, в моей интерпретации, суть его Аналитики сводится к следующему правилу:

Достоверны лишь те высказывания человека, которые проявляют матрицу представлений, символически (и не разделяя варианты на фигуры) это записывается так:

IIA

OOE

OOE. 

То есть:

AAA, AOO, OOA, IOE, EOI, AII, IIA, AEE, EEA, IOO, OOI, OOE, EOO. 

Как это понять?

Два человека спорят. 

Аристотель первым разложил этот спор на базовые термины (позже их назовут семиотическими знаками). Один собеседник - задаёт вопрос, указывая на противоречия в словах другого собеседника, а другой высказывает аргумент отсутствия в его словах таких противоречий. Если они достигают третьего термина - консенсуса (концепта двух точек зрения, дицента, силлогизма, по указанному выше правилу), то спор - сам собой - прекращается, собеседники проявили силу своего мышления и поняли (признали) друг друга. Больше им спорить не о чем, они доверяют друг другу, силлогизм построен и испарился аристотелевым эфиром в небеса. 

Если же силлогизм не построен (взаимного доверия не возникло), но спор продолжается, то это пустая риторика (софизм), попытка подчинить одно мышление другому. Прав тот, чьё мышление сильнее (изворотливее). Это схема обмана одного человека другим, мошенничество. Никакого эфира достоверности не возникает, в небеса ничего не испаряется и собеседники сами не понимают, что говорят. 

Мошенникам обидно читать такие определения их  высказываний, поэтому и возникли альтернативные теории, где чёрное названо белым, но не полностью, а лишь на три четверти, сохраняя видимость достоверности. Это и есть современная формальная логика. Современной она была во времена Теофраста.

В формальной логике аристотелевского естественного основания спора просто нет, спор абстрактен и в двух третях случаев логическая ошибка названа истиной. 

За подробностями отправляю читателя к оригинальному тексту Аналитики. Общедоступный текст испорчен комментариями формальных логиков (накопившимися за две с половиной тысячи лет), формальная логика всего на столетие младше Аналитики, сразу предупреждаю, что читателю прийдется реконструировать оригинальный текст Аристотеля - самостоятельно. Это возможно. 

Совпадение формальной логики с Аналитикой - только на четверть, на три четверти - формальная логика противоречит Аналитике. 

А, так называемые - три закона формальной логики (за исключением четвёртого закона - необходимости достаточного основания - Лейбница) - упрощение уже самой формальной логики. 

Я понимаю логический закон Лейбница - иронией по отношению к достоверности формальной логики, утратившей аристотелевском достаточное основание - естественный анализ общепринятых - в его время - представлений человека о своём мышлении. Но, и эту иронию по отношению к себе самой, формальная логика превратила в свою фальшивую аксиому. 

Чем пять геометрических аксиом Евклида - принципиально - отличны от трёх (четырёх) аксиом формальной логики?

Другой пример - альтернативной (евклидовой) - элементарной геометрии. 

Варшавско-гарвардско-калифорнийская аксиоматика Альфреда Тарского (Тайтельбаума), университет Беркли. 

Собственно, это уже не сколько формальная геометрия, сколько альтернативная логика, как часть философии. Тарский оспорил теорему Гейделя о неполноте и создал теорию невыразимости истины. Уже интересно. Но, очень напоминает новый неософизм (постмодерн). 

Лежать между - отношение, наподобие умножения, деления и так-далее. (Любопытно! Сочетание двух элементов - как обобщение арифметических операторов.) Конгруэнтроность (развитие понятия равенства для геометрических фигур). 

1) Рефлективность конгруэнтности. AB=BA 

(в скобках мой комментарий - у Тарского это уже отказ от понятия спина, AB и BA - разные спины, если они равны, то это значит только одно - понятие спина игнорируется:

А-10 - одна крайность, икона, один (второстепенный - например - не претендент на вершину угла) край отрезка, 

B-01 - другая крайность, символ, другой (первостепенный - претендент на вершину угла) - край отрезка, 

AB-11 - концепт крайностей (сам отрезок, и то и другое одновременно), первый вариант (спин) отрезка, 

BA-00 - второй вариант (спин) отрезка, мнимый концепт (мнимый отрезок) - симулякр концепта - ни то, ни другое).

Причём, какой из вариантов отрезка - концепт, а какой его симулякр - AB или BA - неопределено. Как и - в чем формальное отличие концепта от его симулякра. Противоречие снимается, если считать, что это два разных спина, два разных отрезка между двумя точками. От первой ко второй и от второй к первой. 

Но, в любом случае, тождественность AB и BA - то есть - отказ от понятия спина - условие построения геометрии Тарского. 

Но, даже Аристотель, лишь умолчал о спине, назвав средний элемент - неопределённым, не уточнив - в чем именно заключается такая его неопределенность. 

Кроме того, Аристотель рассуждал об оборачиваемости терминов, как раз - о различии путей AB и BA, которая совсем не однозначна. Отождествлять AB и BA - явное следование упрощениям формальной логики. Игнорирование Аналитики.)

2) Тождественность конгруэнтности. 

/- Здесь я так-же вижу противоречие с представлениями человека о природе, например, о природе субатомных частиц. 

Если атом рассматривать абстракцией - точкой (в фазовом пространстве, в матрице), где - пересечения двух равноценных и перпендикулярных друг другу отрезков (протон-электрон и нейтрон-условное нейтрино, это иллюстрация формулы супругов Кюри), то очевидно, что такие атомы возможны и для других отрезков. Через такую "точку атома" (в фазовом пространстве его характеристик) можно провести множество разных отрезков. 

А, если атом рассматривать числом, то такие числа могут быть получены множеством разных способов.

Аксиома Тарского - косвенно - говорит о том, что все такие атомы - равны. Требуется уточнение - в представлениях человека. На самом деле, они могут быть разными. 

Превращение протона в нейтрон и наоборот - для мышления человека - неразличимо, что понимается нами - фундаментальным сильным взаимодействием. 

Если, применительно к данному случаю верна аксиома AB=BA, то сильное поле типа АB (превращения протона в нейтрон) и другое обратное поле типа BA (превращения нейтрона в протон) - должны быть равны. Что и объясняется нами (самим себе) - сильным взаимодействием - условным отрезком между протоном и нейтроном.  

Если эта аксиому Тарского считать ложной, то и представление о сильном поле - будет ложно. И на смену - общепринятой сейчас - концепции такого поля - прийдет другая. 

На самом деле, то, что может быть представлено кристаллической решёткой одинаковых элементов - на самом деле - может оказаться чем-то принципиально другим, как и хаос атомов в плазме - может оказаться кристаллической решёткой (фазового пространства характеристик), мы не можем отрицать такую возможность. 

Пример такой упорядоченности хаоса - странные атракторы "геометрии хаоса" (в оригинале - "геометрии природы") Бенуа Мандельброта. 

Такого типа примеров мы можем обнаружить много...

Наши представления могут измениться в будущем (или в следствие реконструкции забытого знания из прошлого, например даосской комбинаторики, Аналитики Аристотеля или теории систем отсчета Ньютона, по всей видимости в список возрождаемого знания следует уже отнести и квантовую механику Планка и семиотику Пирса - это знание конца 19-го века и квантовую хромодинамику 1960-х) и мы поймём все иначе.

Аксиома Тарского не то, что бы лишает нас такого права, пытается лишить, но лишить не может. -/

3) Транзитивность конгруэнтности. Операции над множествами: если a=c и b=c, то a=b и так-далее... (Я вижу в этом - интерпретацию рассуждений Аристотеля о "фигурах" - здесь в контексте "композиция терминов", о типах вложения одного термина в другой. Оригинал всегда лучше.)

4) Точка хх (между х и х) - и есть х. (Интересная аксиома, напоминает свойство элементов квантового регистра, как-бы один элемент квантового регистра не сочетался сам с собой, самим собой он и останется).

5) Аксиома Паша, две диагонали прямоугольника должны пересекаться - в одной точке. 

/- Это не справедливо для матрицы - условного геометрического представления множества сочетаний  элементов квантового регистра, в котором диагоналей прямоугольника - с учётом спина - четыре и пересекаются они - потому - в двух точках. Но, становится справедливо, если представить матрицу - фазовым пространством физических величин (представлений человека о них) и если представить каждую грань такого условного куба - двусторонней. 

Должен сразу сказать, что физические величины - в матрице - представляют собой условие лучи, проходящие через центр матрицы, единичку или точку аннигиляции противополных качеств (1/x x x=x/x=1 - точка невыраженного никак фазового состояния физического вакуума).

Эти лучи сочетаются, образуя новые лучи-величины, на подобие векторной суммы. То есть матрица - лучистая сфера, образно - звезда. Но есть одно важное замечание. Эти лучи - как-бы - двойные или двусторонние - многоспиновые. И, если мы пытаемся сочетать односпиновые лучи, проходящие из центра матрицы через элементы квантового регистра - мы не получаем базовые лучи (массы, времени и расстояния), но только их квадраты. А сочетая квадраты, получаем четвертую степень. 

Степень величины это радиус луча сферической матрицы. Все, что меньше нулевой степени величины, умноженное на единицу центра матрицы и есть сама такая величина, но сочетание луча с самим собой - его квадрат и так-далее.

Спин - это многовариантность или неопределенность результата, но неопределенность она только в случае игнорирования спина. На самом деле все точно и однозначно, все варианты просчитываются, пусть это и требует усилий...

Как представить такую неоднозначность визуально?

Аппелирую к вашей фантазии. 

Четвёртым логарифмическим измерением? Листами капусты (слоями или оболочками матрицы), двусторонними линиями и поверхностями? Восьмигранными точками?

Все это условности, предоставляйте как угодно, как вам самим удаётся понять это.

Таким образом, мы имеем по 4 спина массы, расстояния и времени. По две точки на пересечение диагоналей каждой из 6 граней куба. 

В ньютоновской специальной механике (теории систем отсчета) - это те самые системы отсчета. Которые взаимодействуют друг с другом. Внешняя левая грань с внутренней нижней. 

Такое сложное физическое понятие, матрицы-5 (четвёртой степень регистра - 12 бит) как, например - сила, обладает 4 спинами (2 вариантами пересечения диагоналей грани), но только относительно определённого спина частоты (обратного времени - 1/t), с учётом четырёх спинов такого времени (систем отсчета) - сил - 4 х 4= 16 (восемь систем отсчета). И лишь взаимодействие двух из них есть гравитация, но каких именно 2-х из 8? Неопределено. 

Получается, что должно быть множество разных типов гравитации - не считая взаимодействия более, чем двух систем отсчета. 

Рассмотрим силу (sm/t2=221 в матрице-5, в двоичном коде - 000000000011, это один из спинов).

F=ma=I2=F x 1=F2 x 1/F=S/t=m/t x s/t=h/t2=E/s=Ps2=Gm2/s...

Сколько величин мы рассматриваем в матрице - столько возможно и определений силы. И так для любой величины. 

Закон сохранения энергии - частный случай такой симметрии матрицы. 

E=Sv=mc2=h/t=F2t2/m=Гt2/m=Г/(m/t2)=PV=ST=B2V...

B2=Гt2/Vm=Г/v2q2

Г=q2V2B2=F(L)2

q2=Г/B2c2=s2m2t4s/t4ms2=sm

Конечно, может показаться абсурдным представление множества вариантов бит геометрически, если изначально определено, что структура информации - принципиально - точно не представима геометрически.

Не совсем так, не представима только евклидовой геометрией. 

В других альтернативных версиях элементарной геометрии такая возможность начинает формироваться: это идея Александрова рассматривать геометрические объекты как множества, и даже аксиома Паша из геометрии Тарского - для физических величин - видимо - справедлива для каждой из сторон грани матрицы - двустороннего прямоугольника (двустороность здесь - лицо и оборот). 

Но, с более общей точки зрения (геометрического представления информации), точек пересечения диагоналей прямоугольника - четыре. -/

6) Далее у Тарского следуют аксиомы непрерывности. 

"Если F(x) и f(y) описывают два множества точек луча с вершиной a, первое из которых левее второго, то найдётся точка b между этими множествами". (Непараллельные прямые - пересекаются)

Оценка нижней размерности. 

 

"Существуют три неколлинеарные точки. Без этой аксиомы, теории могут быть смоделированы с помощью одномерной вещественной прямой, в одну точку, или даже пустое множество".

 

/- Безусловно, природный - условно (в фазовом пространстве своих характеристик) - трёхмерный объект, пример - состоящая из трёх кварков субатомная частица адрон (шесть бит - варианты: протон, нейтрон, омега минус и т.п) - может быть представлена сочетанием двух глюонов, то есть одновременно быть представленной двумерным объектом (шесть бит). И далее - до линейного сочетания шести бит. 

 

Шесть бит - 000000, можно представить:

 

- шестью группами по одному биту - 0 0 0 0 0 0;

- двумя группами по три бита - 000 000;

- тремя группами по два бита - 00 00 00;

- одной группой шесть бит - 000000;

- другими вариантами.

 

Размерность всех этих вариантов (число условных групп) - различна, но природный объект один и тот-же. Тарский утверждает обратное.

 

Но, своими аксиомами он определяет лишь элементарную геометрию, а геометрия информации - не элементарная. 

 

Тем не менее, мы не должны забывать, что элементарная геометрия - частный случай неэлементарной. И, если мы хотим её представить, то в своих частных случаях она не должна противоречить - ни геометрии Евклида, ни геометрии Александрова, ни геометрии Тарского, ни какой либо иной элементарной геометрии.

 

Чем больше противоречий мы обнаружим между природным процессом и элементарной геометрией его описания, тем точнее мы определим неэлементарную геометрию природы.  -/

6.3) Верхняя оценка размерности.

"То есть любые три точки, равноудаленные от двух различных точек лежат на прямой. Без этой аксиомы, теории может быть применен в трехмерном или более-мерном пространстве."

6.4) Аксиома о пятом отрезке.

"То есть, если 4 пар отрезков на двух чертежах равны то и пятая пара отрезков равна между собой."

6.5.) Построение отрезка.

"То есть, для от любой точки в любом направлении можно отложить отрезок данной длины."

 

Аксиоматика Давида Гильберта (Кёнигсбергский и Геттингенский университеты). 

Конечно, теорема Гёделя 1931 года "о неполноте" привела геометрическую аксиоматику к фиаско, но именно Гильберт в ответ на это сказал: «Любая теория проходит три фазы развития: наивную, формальную и критическую».

Неопределённые (базовые) понятия: 1-точка, 2-прямая (линия), линия, 3-плоскость. (Производные от базовых) понятия: 4-отрезок, 5-угол, 6-треугольник) и так далее.

Три отношения: Лежать между - применимо к 1-точкам. Содержать - применимо к двум из трёх неопределимых понятий (12, 13, 23). Конгруэнтность (геометрическое равенство) - применимо к 4, 5, 6.

Через две точки можно провести прямую и только одну. Каждой прямой принадлежат - как минимум две точки. Существуют три точки не принадлежащие одной прямой. Через три точки, не принадлежащие одной прямой можно провести не более одной плоскости. Плоскость содержит как минимум одну точку. Две различные точки прямой, принадлежат плоскости. Плоскости принадлежит не менее двух точек. Существуют - как минимум - 4 точки не принадлежащие одной плоскости. Если одна точка лежит между двумя другими на прямой, то все три точки принадлежат одной прямой. Между двумя точками прямой всегда найдётся третья точка, как и точка, между которой и одной из прежних находятся рассматриваемые точки. Среди любых трёх точек прямой только одна лежит между крайними. 

Далее Гильберт рассматривает уже знакомую читателю аксиому Паша. Диагонали прямоугольника пересекаются в одной точке.

Продолжаем. 

"Если А и В — две точки на прямой а, А’ — точка на той же прямой или на другой прямой а’, то по данную от точки А’ сторону прямой а’ найдется, и притом только одна, точка В’ такая, что отрезок А’B’ конгруэнтен отрезку АВ. Каждый отрезок АВ конгруэнтен отрезку ВА."

"Если отрезки А’B’ и А"B" конгруэнтны одному и тому же отрезку АВ, то они конгруэнтны и между собой."

"Пусть АВ и ВС — два отрезка прямой а, не имеющие общих внутренних точек, А’B’ и B’C’ — два отрезка той же прямой, или другой прямой а’, также не имеющие общих внутренних точек. Тогда если отрезок АВ конгруэнтен отрезку А’B’, а отрезок ВС конгруэнтен отрезку B’C’, то отрезок АС конгруэнтен отрезку А’C’."

"Если даны угол ∠ABC и луч B’C', лежащий в плоскости данного угла, тогда существует ровно два луча, также лежащие в плоскости данного угла, B’D и B’E, такие, что ∠DB’C' ≅ ∠ABC и ∠EB’C' ≅ ∠ABC. Следствие. Каждый угол конгруэнтен сам себе."

"Если для двух треугольников ABC и A’B'C' имеют место конгруэнции: AB≅A’B', AC≅A’C', ∠BAC ≅ ∠B’A'C', то всегда имеют место и конгруэнции: ∠ABC ≅ ∠A’B'C' ∠ACB ≅ ∠A’C'B'."

"Пусть a есть произвольная прямая и A — точка вне её; тогда в плоскости, определяемой точкой А и прямой а, можно провести не более одной прямой, проходящей через A и не пересекающей a."

"Аксиома Архимеда. Если даны отрезок CD и луч AB, то существует число n и n точек A₁,…,A_n на AB таких, что: A_jA_j+1 ≅ CD, 0<=j<n, A₀ совпадает с A, и B лежит между A и A_n."

_{«Полнота линии». Добавление хотя бы одной дополнительной точки в прямую линию вызовет противоречие с одной из аксиом принадлежности, порядка, первыми двумя аксиомами конгруэнтности или} аксиомой Архимеда."

Сложно критиковать или как-то комментировать аксиоматику Гильберта, после его самоироничного признания фиаско аксиоматики. Но, такая аксиоматика когда-то была актуальной  и по прежнему  представляет историческую ценность, как рассказ об истории науки. 

(Простая и понятная даже школьнику) аксиоматика Биркгофа. Геометрия гарвадского и чикагского университетов. 

Точки прямой представимы вещественными числами. Через две различные точки можно провести только одну прямую. Множество лучей, проходящих через некоторую точку  представимо множеством вещественных чисел по модулю 2 пи... Далее, Биркгоф развивает свою мысль для треугольников. 

 

Теореме Гёделя о неполноте. 

"Теорема Гёделя о неполноте и вторая теорема Гёделя^{[~ 1]} — две теоремы математической логики о принципиальных ограничениях формальной арифметики и, как следствие, всякой формальной системы, в которой можно определить основные арифметические понятия: натуральные числа, 0, 1, сложение и умножение.

Первая теорема утверждает, что если формальная арифметика непротиворечива, то в ней существует невыводимая и неопровержимая формула.

Вторая теорема утверждает, что если формальная арифметика непротиворечива, то в ней невыводима некоторая формула, содержательно утверждающая непротиворечивость этой арифметики.

Обе эти теоремы были доказаны Куртом Гёделем в 1930 году (опубликованы в 1931) и имеют непосредственное отношение ко второй проблеме из знаменитого списка Гильберта."

/- Если рассматривать аксиоматику элементарной геометрии - жанром формальной логики, то и безо всяких теорем очевидна её неполнота по отношению к силлогистике (Аналитике) Аристотеля, ведь (я пояснил это выше) - формальная логика - частично - её упрощение, а по большей части - откровенная подделка Аналитики. Сведение Аристотелева пространства терминов (в котором читается информационное пространство сочетаний даосских стихий природы, но при умалчивании роли спина, хотя он и не отрицается) - к проекции этого пространства на его грань предельно категоричного высказывания. Тень объекта, к тому-же - искажённая (фигуры то перепутаны!), по отношению к самому объекту -  не полна. Это очевидно. 

Основанием своей теории Аристотель рассматривал общепринятые представления своих современников о собственном мышлении. Любая интерпретация Аналитики - не о природе, но о природе представлений человека о природе своего ума... Нетрезво выводить из таких представлений хоть какие-то аксиомы. 

Но, культура переинтерпретации и есть именно такой нетрезвый взгляд. В определённый момент - у честного человека - наступает отрезвление, пример - загадки Гильберта и решение некоторых из них Геделем. Опьянение длились почти две с половиной тысячи лет. 

Конечно, Аналитика начинается с рассмотрения оборачиваемости терминов, это и есть историческая основа аксиоматики. Но, Аристотель (в отличие от его читателей и интерпретаторов) - быстро преодолевает этот этап и приходит к матрице терминов. Читатель так и застревает на аксиоматике, испытывает смысловые галлюцинации сказать все проще... 

Основанием Аналитики является естественность представлений человека о своём мышлении. Структурно - это силлогизмы. Суждения, проявляющие структуру пространства суждений. 

Любое доказательство основано на силлогизмах, но сам силлогизм доказательством не является. Аристотель рассмотрел его сутью общепринятого в его время представления человека о самом себе. Аксиоматика - поиск альтернативного основания, которое так и нашлось. 

Этот вопрос я рассмотрел выше. Здесь - возвращаюсь к нему только в качестве комментария к аксиоматике элементарной геометрии и фиаско такой традиции в 1931 году. Что ничуть не помешало созданию альтернативных систем аксиом. 

Почему? 

Потому, что аксиоматика не только развивает формальную логику, но и пытается вскрыть и устранить её ошибочность. Это можно назвать смутным видением матрицы, которую Аристотель уже однажды описал, но не был понят. Его теория вырвала длительные смысловые галлюцинации. Хотя и сам Аристотель - лишь приближался к даосской матрице стихий природы, как и Платон. Именно поэтому, Фома Аквинский, в 13-м веке определил благодать - как непротиворечивое единство обоих версий приближения к даосскому пониманию мышления человека, версии Платона и версии Аристотеля. -/

Неевклидова (новая) геометрия середины 19-го века. 

Неевклидова геометрия - любая геометрическая аксиоматика, отличная от евклидовой (с2=а2+b2).

Сферическая геометрия - c2=a2+cos2(b/R)b2, где R  - радиус сферы. Для такой геометрии и её производных (Римана) - отсутствует непротиворечивое понятие средней точки.

Геометрия Лобачевского - c2=a2+ch2(b/R)b2, где ch - гиперболический косинус, а R - радиус кривизны плоскости Лобачевского. 

Геометрия Римана - многомерная сферическая геометрия. Её развитием стало тензорное исчисление, реализованное, в частности - в теории относительности Эйнштейна. 

По сути - теория относительности есть подгонка физики под неевклидову тензорную геометрию. Если евклидова плоскость искривлена, то что же является природным феноменом такого искривления? Скорость, масса? Остальное - дело техники. Удивительно, но эксперимент подтвердил откровенную авантюрную теорию. 

Почему? 

По тому, что такая теория, естественным образом и вопреки методологии - приблизилась к - пусть и упрощенному - но к поминанию информационной матрицы вселенной. 

Информационная, матричная или квантовая геометрия - не сколько обобщение прочих геометрий, сколько реконструкция прото-геометрии - как даосской комбинаторики и Аналитики Аристотеля. 

Но, такая постмодернистская деконструкция геометрии не была единственной и потому её - условно - можно назвать обобщением других попыток реконструкции Аналитики. 

Как таковой  аксиоматики, подобной евклидовой и неевклидовой - у информационной геометрии уже нет. Любая точная аксиоматика рассматривается смысловой галлюцинацией. Не может рассматриваться всерьёз, вне её социальной пользы. Которая не считается достойной целью знания. 

Исторически - из всех возможных теорий - университет фильтровал только те, что поддерживали его статус социальной институции. История открытий случайна и непредсказуема, духовное открытие может произойти когда угодно и где угодно, университет лишь очень неэффективная Сеть трансляции таких инсайдов Бытия. История науки отредактирована, и не будь у человечества социальных пут - на подобие университета и подражания ему - государства - прогресс науки, техники и искусства шёл бы куда быстрее. 

Любая теория объекта не равна объекту только лишь по формальному признаку. Если человеку удаётся добиться единства означающего (смыслоформы своей идеи Бытия) и означаемого (самой такой трансцендентной идеи) - любая такая метафора Бытия достойна внимания. Как её воспримут слушатели - так и воспримут, наверняка - как-то по своему. 

Социальный успех той или иной теории - это цепочка переинтерпретаций, далёких от первоначального смысла. Поэтому, успех - случайность и никак не связан с достоверностью самой теории. 

Есть представление человека о собственном мышлении, как об условно геометрическом объекте и такое представление служит лишь иллюстрацией его идеи.  Важнее понять, что человеку можно доверять. А признаком такой достоверности случит чёткое представление Бытия - не важно какими именно метафорами. 

Аксиоматика таких представлений Бытия возможна, но она - не более чем одна из возможных интерпретаций. Если кто-то видит в ней удобную для выражения своей идеи форму - почему бы нет. Но, рассматривать такую аксиоматику универсальным базисом - больше не стоит, сколько людей, столько и мнений. 

Бытие - в квантовой или информационной геометрии - условно представляется точкой аннигиляции всех качеств, физически это вакуум. 

Естественным образом, человек разделяет (в своём мышлении) - такую начальную точку своих представлений о природе на крайности (свет и тьму, Инь и Ян) и, как-бы мысленно проводит через неё условную прямую, начальная точка делит такой луч - логарифмический (его отметки - степени величины) - на прямое (х или 1) и обратное (1/х или 0) качество. В двоичной записи это ноль или единица - бит - базовая неопределенность. 

Исторически так сложилось, что западная традиция аналитики, со времен античности, как правило - рассматривает трехмерное фазовое пространство таких качеств - расстояние, масса и время. В контексте структуры мышления - это тип высказывания (форма идеи), посылка (смысл) и степень категоричности (дефиниция). В квантовой хромодинамике - это три абстрактных цвета кварков - красный, зелёный, синий. Это три основные луча, исходящие из начальной точки Бытия по углам 90 градусов по отношению друг другу. Базис можно сместить, совершив поворот матрицы. Все прочие феномены представляются - в западной традиции - комбинаторикой таких лучей. 

Если ограничить эти три базовые луча с обоих сторон каждый, и рассмотреть все возможные сочетания шести таких точек, то это будет квантовый регистр, восемь даосских стихий природы:

000-чёрная земля, 001-синяя гора, 010-зелёная вода, 011-голубой ветер, 100-красный гром, 101-фиолетовый огонь, 110-жёлтая пропасть, 111-белое небо. 

Физический контекст таких стихий я привёл выше. Например, кварки и есть такие логарифмические отметки (исторически по основанию 10) на трёх базовых осях абстрактного цвета ядерных физиков. 

Сочетание элементов квантового регистра - трёх бит - создаёт матрицу терминов (по Аристотелю) или матрицу семиотических знаков (по Пирсу). Физически - это квадраты базовых величин. 

Вместо долгого и мучительного творческого и экспериментального открытия новых элементов (лучей и отметок на них ), рассматривается история открытия человеком различных участков матрицы и история усложнения представлений о матрице. 

Культура принципиально (так она устроена) отрицает матрицу мышления, но использует её вторичные упрощённые образы в социальной жизни. Поэтому гораздо важнее использование матрицы достоверности (ещё одно её историческое название) в собственном творчестве, в качестве своего рода нити Ариадны или мифологической картины мира. Матрицу, как идею можно выразить лишь авторской метафорой. Возможно лишь последовательное содействие человечеству в освоении матрицы. Доказывать её справедливость не кому и не зачем. Все доказательства - частные случаи такой матрицы. 

В любом случае - матрица есть условность. Более точное представление Бытия - цепочки бит. Но, благодаря матрице возможно находить внутренние связи цепочек знаков. 

Ещё одна, третья, по отношению к двоичной битовой и условно-геометрической метафорам - метафора нейронной сети. 

Любой текст состоит из групп бит, три бит - это квантовый регистр, шесть бит - это знак, два квантовых регистра, 12 бит - дискурс, два знака и так-далее. Так вот, любое условное геометрическое представление битового текста позволяет визуализировать неразличимые в самом тексте внутренние связи между группами бит. По сути - разгадывать любой шифр. 

Текст представим нейронной сетью знаков. И все тексты - части одного текста, ни один текст не кончается и не начинается. Лишь один знак добавляется к предыдущему, усложняя нейронные связи. 

Такие связи можно оборвать или подменить поверхностными признаками, это задача культуры, но как в природе, найдутся обходные пути, природа все равно возьмёт своё. 

Нейрон человеческого мозга обладает - в среднем - 4096 отростками, связывающими его с другими нейронами, то есть, он условно представим дискурсом (множеством двух знаков или четырёх регистров - 12 бит). 

Сочетание двух и более регистров геометрически условно представимо детализацией квантового регистра. В геометрическом представлении информации, знаки как-бы накладываются друг на друга, добавляя регистру новые детали. Бесконечно подробная матрица и есть Бытие. Каким человек способен его познать.

Сама жизнь человека - такие цепочки знаков. Все, что человек говорит и делает, можно записать двоичным кодом. Условная геометрическая матрица знаков позволяет посмотреть на человека со стороны, трезво и объективно. И, такое инсайдерское знание, не понятное подавляющему большинству людей является источником духовной энергии всего человечества. В конечном итоге - оно делает жизнь человека полнее, приводит к инженерным и прочим творческим открытиям. Делает мир лучше.

Продолжение следует.

 

Отправлено с iPad